
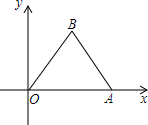
 等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.分析 (1)如图1所示过点B作BC⊥OA,垂足为C.由等边三角形的性质和特殊锐角三角函数值可知OC=1,BC=$\sqrt{3}$,从而可求得点B的坐标;
(2)如图2所示,根据平行线的性质和旋转的定义可确定出a的值;
(3)利用旋转的性质可知A1B1=2,从而可求得点B1的值.
解答 解:(1)如图1所示过点B作BC⊥OA,垂足为C.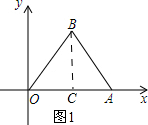
∵△OAB为等边三角形,
∴∠BOC=60°,OB=BA.
∵OB=AB,BC⊥OA,
∴OC=CA=1.
在Rt△OBC中,$\frac{BC}{OC}=\sqrt{3}$,
∴BC=$\sqrt{3}$.
∴点B的坐标为(1,$\sqrt{3}$).
(2)如图2所示: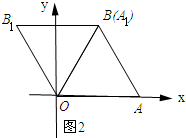
∵点B1与点A1的纵坐标相同,
∴A1B1∥OA.
①如图2所示:当a=300°时,点A1与点B1纵坐标相同.
如图3所示: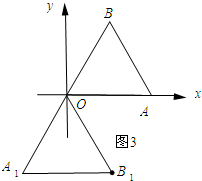
当a=120°时,点A1与点B1纵坐标相同.
∴当a=120°或a=300°时,点A1与点B1纵坐标相同.
(3)如图2所示:由旋转的性质可知A1B1=AB=2,点B的坐标为(1,2),
∴点B1的坐标为(-1,$\sqrt{3}$).
如图3所示:由旋转的性质可知:点B1的坐标为(1,-$\sqrt{3}$).
∴点B1的坐标为(-1,$\sqrt{3}$)或(1,-$\sqrt{3}$).
点评 本题主要考查的是旋转的性质,等腰三角形的性质、等边三角形的性质,掌握相关性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
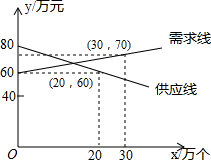 某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?
某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
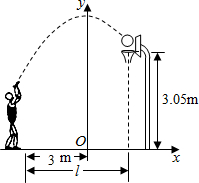 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com