
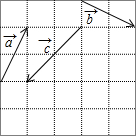
 如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作:
如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作:分析 (1)根据图示写出向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,然后根据向量的加法法则进行计算即可;
(2)根据图示写出向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,然后根据向量的减法法则进行计算即可.
解答  解:如图所示,$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-1),$\overrightarrow{c}$=(-2,-2).
解:如图所示,$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-1),$\overrightarrow{c}$=(-2,-2).
(1)$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=(1+2-2,2-1-2),即$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=(1,-1);
(2)$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{c}$=(1-2+2,2+1+2),即$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{c}$=(1,5).
点评 本题考查平面向量的坐标运算,解题的关键是读懂图中给予的已知条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
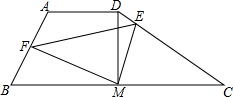 如图,在梯形ABCD中,AB<CD,M为BC中点,且DM⊥BC于M,∠B+∠C=90°,动点F从点B出发沿线段BA方向以$\sqrt{3}$厘米/秒的速度运动,点E从点D出发沿DC方向运动,且始终保持EM⊥FM,当点F到达点A时停止运动或当点E到达点C时停止运动.设运动时间为t(t>0)秒.
如图,在梯形ABCD中,AB<CD,M为BC中点,且DM⊥BC于M,∠B+∠C=90°,动点F从点B出发沿线段BA方向以$\sqrt{3}$厘米/秒的速度运动,点E从点D出发沿DC方向运动,且始终保持EM⊥FM,当点F到达点A时停止运动或当点E到达点C时停止运动.设运动时间为t(t>0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
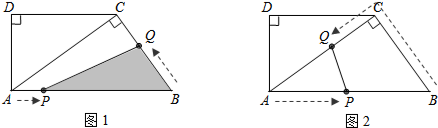
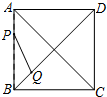 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )
如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )| A. | 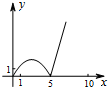 | B. | 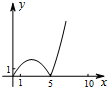 | C. | 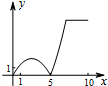 | D. | 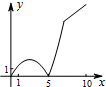 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com