
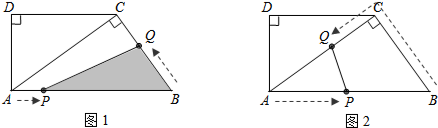
分析 (1)①根据DC∥AB,得到∠ACD=∠BAC,由于∠D=90°,AC⊥BC,于是得到∠D=∠ACB=90°,就可得到△ACD∽△BAC;
②在Rt△ABC中,由勾股定理得AC=$\sqrt{A{B^2}-B{C^2}}=\sqrt{{{10}^2}-{6^2}}$=8(cm),根据△ACD∽△BAC,列比例式即可得到结果;
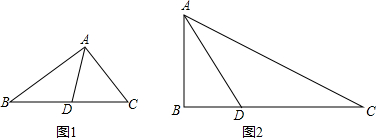
(2)如图1,点Q在边BC上运动,此时,0<t≤3,过点Q作QE⊥AB于E,根据三角函数sinB=$\frac{QE}{QB}=\frac{AC}{AB}$,即 $\frac{QE}{2t}=\frac{8}{10}$,求得QE=$\frac{8}{5}$t,根据三角形的面积列方程即可得到结论;
(3)如图2,当点Q在边CA上运动,$\frac{AQ}{AC}=\frac{AP}{AB}$时,PQ∥BC,列比例式得方程解得结果.
解答 解:(1)①∵DC∥AB,
∴∠ACD=∠BAC,
又∵∠D=90°,AC⊥BC,
∴∠D=∠ACB=90°,
∴△ACD∽△BAC,
②在Rt△ABC中,
由勾股定理,得AC=$\sqrt{A{B^2}-B{C^2}}=\sqrt{{{10}^2}-{6^2}}$=8(cm),
∵△ACD∽△BAC,
∴$\frac{DC}{AC}=\frac{AC}{AB}$,
即 $\frac{DC}{8}=\frac{8}{10}$.
解得DC=6.4(cm);
(2)如图1,点Q在边BC上运动,此时,0<t≤3,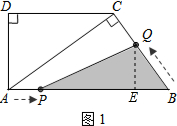
过点Q作QE⊥AB于E,
∴sinB=$\frac{QE}{QB}=\frac{AC}{AB}$,即 $\frac{QE}{2t}=\frac{8}{10}$,
解得 QE=$\frac{8}{5}$t,
∴$\frac{1}{2}$BP•QE=$\frac{1}{2}$(10-t)•$\frac{8}{5}$t=$\frac{64}{5}$,
整理,得 t2-10t+16=0,
解这个方程,得t1=2,t2=8 (不合题意,舍去),
∴当点Q在边BC上运动,t=2s时,△PBQ的面积为$\frac{64}{5}$cm2,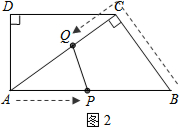
(3)如图2,当点Q在边CA上运动,$\frac{AQ}{AC}=\frac{AP}{AB}$时,PQ∥BC,
∴即 $\frac{14-2t}{8}=\frac{t}{10}$,
解得 t=5.
∴当点Q在边CA上运动,t=5s时,PQ∥BC.
点评 本题考查了相似三角形的判定和性质,解直角三角形,平行线分线段成比例定理,三角形的面积,注意方程思想在本题中的应用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
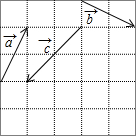 如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作:
如图,由单位小正方形拼成的5×5的大正方形中.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$.求作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com