
如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣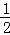 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
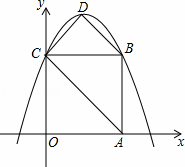
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
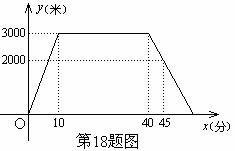
小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小敏离家的路程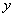 (米)
(米) 和所经过的时间
和所经过的时间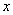 (分)之间的函数图象如
(分)之间的函数图象如 图所示。请根据图象回答下列问题:
图所示。请根据图象回答下列问题:
(1)小敏去超市途中的速度是多少?在超市逗留了多少时间?
(2)小敏几点几分返回到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
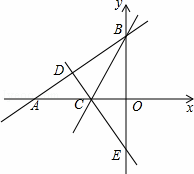
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.
(1)求线段AB的长;
(2)求直线CE的解析式;
(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处 ,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
(1)求OE 的长及经过O,D,C 三点的抛物线的解析式;
(2)一动点P 从点C 出发,沿CB 以每秒2 个单位长的速度向点B 运动,同时动点Q 从E 点出发,沿EC 以每秒1 个单位长的速度向点C 运动,当点P 到达点B 时,两点同时停止运动.设运动时间为t 秒,当t为何值时,DP=DQ;
(3)若点N 在(1)中的抛物线的对称轴上,点M 在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E 为顶点的四边形是平行四边形?若存在,请求出M 点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
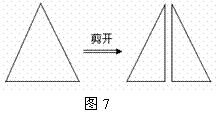
如图7,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,
得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 ____ 个不同的四边形.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com