练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    小敏上午8:00从家里出发，骑车去一家超市购物，然后从这家超市返回家中。小敏离家的路程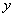（米）和所经过的时间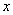（分）之间的函数图象如图所示。请根据图象回答下列问题：

    （1）小敏去超市途中的速度是多少？在超市逗留了多少时间？

    （2）小敏几点几分返回到家？



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


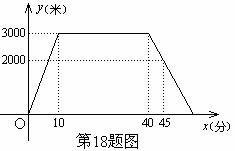
    如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．

    （1）求证：AC是⊙O的切线；

    （2）已知圆的半径R=5，EF=3，求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2014年10月24日，“亚洲基础设施投资银行”在北京成立，我国出资500亿美元，这个数用科学记数法表示为                  美元-1＜x＜0或x＞2

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


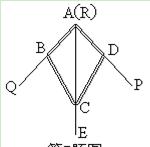
    如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线。此角平分仪的画图原理是：根据仪器结构，可得

    △ABC≌△ADC，这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是

    A. SAS           B. ASA          C. AAS              D. SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB。若PB=4，则PA的长为     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


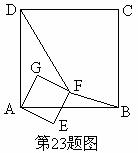
    正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图。

    （1）若α=0°，则DF=BF，请加以证明；

    （2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题；

    （3）对于（1）中命题的逆命题，如果能补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（　　）

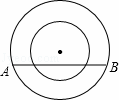
    　 A． 8≤AB≤10 B． 8＜AB≤10 C． 4≤AB≤5 D． 4＜AB≤5

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A、C分别在x轴、y轴的正半轴，抛物线y=﹣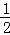x2+bx+c经过B、C两点，点D为抛物线的顶点，连接AC、BD、CD．

    （1）求此抛物线的解析式．

    （2）求此抛物线顶点D的坐标和四边形ABCD的面积．

    　

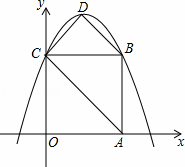
    查看答案和解析>>

    科目：初中数学 来源： 题型：


      的整数部分是　

    查看答案和解析>>

    同步练习册答案