
ЁОЬтФПЁПЗўзАЕъзМБИЙКНјМзввСНжжЗўзАЙВ100МўЃЌЗбгУВЛЕУГЌЙ§7500дЊ.МзжжЗўзАУПМўНјМл80дЊЃЌУПМўЪлМл120дЊЃЛввжжЗўзАУПМўНјМл60дЊЃЌУПМўЪлМл90дЊ.
ЃЈЂёЃЉЩшЙКНјМзжжЗўзА![]() МўЃЌЪдЬюаДЯТБэ.
МўЃЌЪдЬюаДЯТБэ.
БэвЛ
ЙКНјМзжжЗўзАЕФЪ§СП/Мў | 10 | 20 | Ё |
|
ЙКНјМзжжЗўзАЫљгУЗбгУ/дЊ | 800 | 1600 | Ё | |
ЙКНјввжжЗўзАЫљгУЗбгУ/дЊ | 5400 | Ё |
БэЖў
ЙКНјМзжжЗўзАЕФЪ§СП/Мў | 10 | 20 | Ё |
|
МзжжЗўзАЛёЕУЕФРћШѓ/дЊ | 800 | Ё | ||
ввжжЗўзАЛёЕУЕФРћШѓ/дЊ | 2700 | 2400 | Ё |
ЃЈЂђЃЉИјГіФмЙЛЛёЕУзюДѓРћШѓЕФНјЛѕЗНАИЃЌВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ,4800ЃЌ
,4800ЃЌ![]() ,400ЃЌ
,400ЃЌ![]() ,
,![]() ;ЃЈЂђЃЉЙКНјМзжжЗўзА75МўЃЌввжжЗўзА25МўЪБЃЌПЩЛёЕУзюДѓРћШѓ,РэгЩМћНтЮі
;ЃЈЂђЃЉЙКНјМзжжЗўзА75МўЃЌввжжЗўзА25МўЪБЃЌПЩЛёЕУзюДѓРћШѓ,РэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉМзЗўзАЕФМўЪ§ГЫвдНјЛѕМлМДЮЊЙКНјМзжжЗўзАЫљгУЗбгУЃЌввЕФНјЛѕМлГЫвдЃЈ100-МзЕФМўЪ§ЃЉМДЮЊЙКНјввжжЗўзАЫљгУЗбгУ;РћШѓ=ЃЈЪлМл-НјЛѕМлЃЉЁСМўЪ§;
ЃЈ2ЃЉЩшЙКНјМзжжЗўзА![]() МўЃЌИљОнЗбгУВЛЕУГЌЙ§7500дЊЃЌЧѓГіxЕФЗЖЮЇЃЌШЛКѓЧѓГіРћШѓЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌдйгЩКЏЪ§ЕФаджЪЧѓГізюжЕМДПЩ.
МўЃЌИљОнЗбгУВЛЕУГЌЙ§7500дЊЃЌЧѓГіxЕФЗЖЮЇЃЌШЛКѓЧѓГіРћШѓЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌдйгЩКЏЪ§ЕФаджЪЧѓГізюжЕМДПЩ.
ЃЈЂёЃЉБэвЛ
ЙКНјМзжжЗўзАЕФЪ§СП/Мў | 10 | 20 | Ё |
|
ЙКНјМзжжЗўзАЫљгУЗбгУ/дЊ | 800 | 1600 | Ё |
|
ЙКНјввжжЗўзАЫљгУЗбгУ/дЊ | 5400 | 4800 | Ё |
|
БэЖў
ЙКНјМзжжЗўзАЕФЪ§СП/Мў | 10 | 20 | Ё |
|
МзжжЗўзАЛёЕУЕФРћШѓ/дЊ | 400 | 800 | Ё |
|
ввжжЗўзАЛёЕУЕФРћШѓ/дЊ | 2700 | 2400 | Ё |
|
ЃЈЂђЃЉЩшЙКНјМзжжЗўзА![]() МўЃЌгЩЬтвтПЩжЊЃК
МўЃЌгЩЬтвтПЩжЊЃК
![]()
НтЕУЃК![]() .
.
ЙКНјМзжжЗўзА![]() МўЃЌзмРћШѓЮЊ
МўЃЌзмРћШѓЮЊ![]() дЊЃЌ
дЊЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЌ
ЕФдіДѓЖјдіДѓЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ
дђЙКНјМзжжЗўзА75МўЃЌввжжЗўзА25МўЪБЃЌПЩЛёЕУзюДѓРћШѓ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЯТСаЫЕЗЈЃЌДэЮѓЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
Ђй![]() ЪЧЗжЪНЃЛЂкЕБxЁй1ЪБЃЌ
ЪЧЗжЪНЃЛЂкЕБxЁй1ЪБЃЌ![]() ГЩСЂЃЛЂлЕБx=Љ3ЪБЃЌЗжЪН
ГЩСЂЃЛЂлЕБx=Љ3ЪБЃЌЗжЪН![]() ЕФжЕЪЧСуЃЛЂмa
ЕФжЕЪЧСуЃЛЂмa![]() ЃЛЂн
ЃЛЂн![]() ЃЛЂо2Љx
ЃЛЂо2Љx![]() ЃЎ
ЃЎ
A.6ИіB.5ИіC.4ИіD.3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
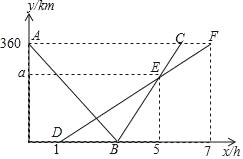
ЁОЬтФПЁППьЁЂТ§СНГЕЗжБ№ДгЯрОр360kmЕФМбЪаЁЂЙўЪаСНЕиГіЗЂЃЌдШЫйааЪЛЃЌЯШЯрЯђЖјааЃЌТ§ГЕдкПьГЕГіЗЂ1hКѓГіЗЂЃЌЕНДяМбЪаКѓЭЃжЙааЪЛЃЌПьГЕЕНДяЙўЪаКѓЃЌСЂМДАДдТЗдЫйЗЕЛиМбЪаЃЈПьГЕЕїЭЗЕФЪБМфКіТдВЛМЦЃЉЃЌПьЁЂТ§СНГЕОрЙўЪаЕФТЗГЬy1ЃЈЕЅЮЛЃКkmЃЉЃЌy2ЃЈЕЅЮЛЃКkmЃЉгыПьГЕГіЗЂЪБМфxЃЈЕЅЮЛЃКhЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌЧыНсКЯЭМЯѓаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉжБНгаДГіТ§ГЕЕФааЪЛЫйЖШКЭaЕФжЕЃЛ
ЃЈ2ЃЉПьГЕгыТ§ГЕЕквЛДЮЯргіЪБЃЌОрРыМбЪаЕФТЗГЬЪЧЖрЩйЧЇУзЃП
ЃЈ3ЃЉПьГЕГіЗЂЖрЩйаЁЪБКѓСНГЕЯрОрЮЊ100kmЃПЧыжБНгаДГіД№АИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮ![]() ЕФБпГЄЮЊ4,Еу
ЕФБпГЄЮЊ4,Еу![]() ЪЧЁї
ЪЧЁї![]() ЕФжааФЃЌ
ЕФжааФЃЌ![]() .ШЦЕу
.ШЦЕу![]() а§зЊ
а§зЊ![]() ,ЗжБ№НЛЯпЖЮ
,ЗжБ№НЛЯпЖЮ![]() гк
гк![]() СНЕуЃЌСЌНг
СНЕуЃЌСЌНг![]() ,ИјГіЯТСаЫФИіНсТл:Ђй
,ИјГіЯТСаЫФИіНсТл:Ђй![]() ;Ђк
;Ђк![]() ;ЂлЫФБпаЮ
;ЂлЫФБпаЮ![]() ЕФУцЛ§ЪМжеЕШгк
ЕФУцЛ§ЪМжеЕШгк![]() ;ЂмЁї
;ЂмЁї![]() жмГЄЕФзюаЁжЕЮЊ6,ЩЯЪіНсТлжае§ШЗЕФИіЪ§ЪЧ( )
жмГЄЕФзюаЁжЕЮЊ6,ЩЯЪіНсТлжае§ШЗЕФИіЪ§ЪЧ( )
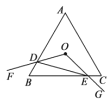
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЗўзАЙЋЫОЪдЯњвЛжжГЩБОЮЊУПМў50дЊЕФ![]() аєЩРЃЎЪдЯњжаЗЂЯжЃЌЕБЯњЪлЕЅМлЪЧ60дЊЪБЃЌЪлГі400МўЃЛЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌЖрЪлГі10МўЃЎЩшЪдЯњжаЯњЪлЕЅМл
аєЩРЃЎЪдЯњжаЗЂЯжЃЌЕБЯњЪлЕЅМлЪЧ60дЊЪБЃЌЪлГі400МўЃЛЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌЖрЪлГі10МўЃЎЩшЪдЯњжаЯњЪлЕЅМл![]() ЃЈдЊЃЉЪБЕФЯњЪлСПЮЊ
ЃЈдЊЃЉЪБЕФЯњЪлСПЮЊ![]() ЃЈМўЃЉЃЎ
ЃЈМўЃЉЃЎ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшИУЙЋЫОЛёЕУЕФзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШєвЊЯњСПВЛЕЭгк200МўЃЌЧвЛёРћжСЩй5250дЊЃЌдђЪлМлгІдкКЮЗЖЮЇФкЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌCDЮЊЁбOЕФЧаЯпЃЌЕуCЪЧЧаЕуЃЎ
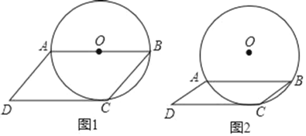
ЃЈ1ЃЉШчЭМ1ЃЌШєABЮЊЁбOжБОЖЃЌЧѓЫФБпаЮABCDИїФкНЧЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєABЮЊЯвЃЌЁбOЕФАыОЖЮЊ3cmЃЌЕБBC=2cmЪБЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮжНЦЌABCDЃЌAB=7ЃЌBC=4ЃЌдкОиаЮБпЩЯгавЛЕуPЃЌЧвDP=3ЃЎНЋОиаЮжНЦЌелЕўЃЌЪЙЕуBгыЕуPжиКЯЃЌелКлЫљдкжБЯпНЛОиаЮСНБпгкЕуEЁЂFЃЌдђEF=__________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌбЇаЃЕФЪЕбщТЅЖдУцЪЧвЛДБНЬбЇТЅЃЌаЁУєдкЪЕбщТЅЕФДАПкCДІВтЕУНЬбЇТЅЖЅВПDДІЕФбіНЧЮЊ18ЁуЃЌНЬбЇТЅЕзВПBДІЕФИЉНЧЮЊ20ЁуЃЌНЬбЇТЅЕФИпBD=21mЃЌЧѓЪЕбщТЅгыНЬбЇТЅжЎМфЕФОрРыABЃЈНсЙћБЃСєећЪ§ЃЉЃЎЃЈВЮПМЪ§ОнЃКtan18ЁуЁж0.32ЃЌtan20ЁуЁж0.36ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвдЕуOЮЊдВаФЕФдВЗжБ№НЛxжсЕФе§АыжсгкЕуMЃЌНЛyжсЕФе§АыжсгкЕуNЃЎСгЛЁ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЎ
гыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂBЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпABгыЁбOЯрЧаЃЛ
ЃЈ2ЃЉЧѓЭМжаЫљЪОЕФвѕгАВПЗжЕФУцЛ§ЃЈНсЙћгУІаБэЪОЃЉ
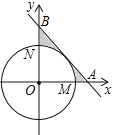
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com