
【题目】已知四边形ABCD是平行四边形,CD为⊙O的切线,点C是切点.
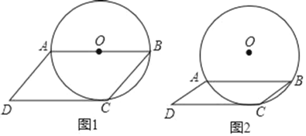
(1)如图1,若AB为⊙O直径,求四边形ABCD各内角的度数;
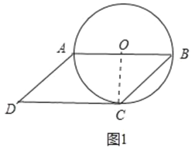
(2)如图2,若AB为弦,⊙O的半径为3cm,当BC=2cm时,求CD的长.
【答案】(1)∠DAB=∠DCB=135°,∠D=∠B=45°;(2)![]() cm.
cm.
【解析】
(1)如图1中,连接OC.只要证明△OCB是等腰直角三角形即可解决问题,
(2)如图2中,连接OC交AB于点E,连接OB,由(1)可知:AB⊥OC,设OE=xcm,则CE=(3-x)cm,构建方程求解,再利用垂径定理即可解决问题.
解:(1)如图1中,连接OC.
∵CD切⊙O于点C,
∴CD⊥OC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB⊥OC,
∵OC=OB,
∴∠B=∠OCB=45°,
∴∠BCD=∠OCD+∠OCB=135°,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=135°,∠D=∠B=45°.
(2)如图2中,连接OC交AB于点E,连接OB,
由(1)可知:AB⊥OC,

∴OB2﹣OE2=BE2,BC2﹣CE2=EB2,
设OE=xcm,则CE=(3﹣x)cm,
![]() OB=3,BC=2,
OB=3,BC=2,
∴32﹣x2=22﹣(3﹣x)2,
∴x=![]() ,即OE=
,即OE=![]() cm,
cm,
∴BE=![]() =
=![]() cm,
cm,
∴AB=2BE=![]() cm,
cm,
∵四边形ABCD 平行四边形,
∴CD=AB=![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A(0,3),点B(﹣3,0),点C(1,0),点D(0,1),连AB,AC,BD.
(1)求证:BD⊥AC;
(2)如图②,将△BOD绕着点O旋转,得到△B′OD′,当点D′落在AC上时,求AB′的长;
(3)试直接写出(Ⅱ)中点B′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进生态文明建设,甲、乙两工程队同时为崂山区的两条绿化带铺设草坪.两队所铺设草坪的面积![]() (米)与施工时间
(米)与施工时间![]() (时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
(时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
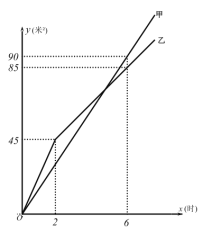
(1)从工作2小时开始,施工方从乙队抽调两人对草坪进行灌溉,乙队速度有所降低,求乙队在工作2小时后![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求乙队降速后,何时铺设草坪面积为甲队的![]() ?
?
(3)乙队降速后,甲乙两队铺设草坪速度之比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店准备购进甲乙两种服装共100件,费用不得超过7500元.甲种服装每件进价80元,每件售价120元;乙种服装每件进价60元,每件售价90元.
(Ⅰ)设购进甲种服装![]() 件,试填写下表.
件,试填写下表.
表一
购进甲种服装的数量/件 | 10 | 20 | … |
|
购进甲种服装所用费用/元 | 800 | 1600 | … | |
购进乙种服装所用费用/元 | 5400 | … |
表二
购进甲种服装的数量/件 | 10 | 20 | … |
|
甲种服装获得的利润/元 | 800 | … | ||
乙种服装获得的利润/元 | 2700 | 2400 | … |
(Ⅱ)给出能够获得最大利润的进货方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() (
(![]() )与抛物线
)与抛物线![]() (
(![]() )交于A,B两点,且点A的横坐标是
)交于A,B两点,且点A的横坐标是![]() ,点B的横坐标是3,则以下结论:①抛物线
,点B的横坐标是3,则以下结论:①抛物线![]() (
(![]() )的图象的顶点一定是原点;②x>0时,直
)的图象的顶点一定是原点;②x>0时,直![]() 线
线![]() 与抛物线
与抛物线![]() (
(![]() )的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当
)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
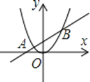
A.①②B.①②⑤C.②③④D.①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
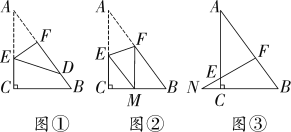
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,AE的长为 ;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,则
,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
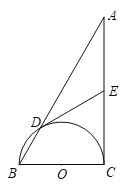
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com