
【题目】如图,直线![]() (
(![]() )与抛物线
)与抛物线![]() (
(![]() )交于A,B两点,且点A的横坐标是
)交于A,B两点,且点A的横坐标是![]() ,点B的横坐标是3,则以下结论:①抛物线
,点B的横坐标是3,则以下结论:①抛物线![]() (
(![]() )的图象的顶点一定是原点;②x>0时,直
)的图象的顶点一定是原点;②x>0时,直![]() 线
线![]() 与抛物线
与抛物线![]() (
(![]() )的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当
)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
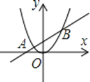
A.①②B.①②⑤C.②③④D.①②④⑤
【答案】B
【解析】
①由顶点坐标公式判断即可;
②根据图象得到一次函数y=kx+b为增函数,抛物线当x大于0时为增函数,本选项正确;
③AB长不可能为5,由A、B的横坐标求出AB为5时,直线AB与x轴平行,即k=0,与已知矛盾;
④若OA=OB,得到直线AB与x轴平行,即k=0,与已知k≠0矛盾,即可求解.⑤直线y=-kx+b与y=kx+b关于y轴对称,作出对称后的图象,故y=-kx+b与抛物线交点横坐标分别为-3与2,找出一次函数图象在抛物线上方时x的范围判断即可.
①抛物线![]() ,利用顶点坐标公式得:顶点坐标为(0,0),本选项正确;
,利用顶点坐标公式得:顶点坐标为(0,0),本选项正确;
②根据图象得:直线![]() 为增函数;抛物线
为增函数;抛物线![]() 当x>0时为增函数,则x>0时,直线与抛物线数值都随x的增大而增大,本选项正确;
当x>0时为增函数,则x>0时,直线与抛物线数值都随x的增大而增大,本选项正确;
③由A、B横坐标分别为-2,3,若 AB=5,可得出直线AB与x轴平行,即k=0,与已知k≠0矛盾,故AB不可能为5,本选项错误;
④若OA=OB,得到直线AB与x轴平行,即k=0,与已知k≠0矛盾,,即△A0B不可能为等边三角形,本选项错误;
⑤直线y=-kx+b与y=kx+b关于y轴对称,如图所示:可得出直线y=-kx+b与抛物线交点C、D横坐标分别为-3,2,
由图象可得:当-3<x<2时,ax2<-kx+b,即ax2+kx<b,
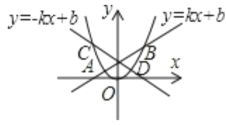
则正确的结论是①②⑤
故选:B


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
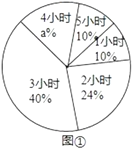
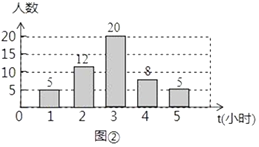
【题目】为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)该校抽查九年级学生的人数为 ,图①中的a值为 ;
(2)求统计的这组数据的众数、中位数和平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
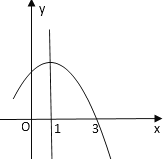
【题目】已知二次函数![]() 的部分图象如图所示,则下列结论:
的部分图象如图所示,则下列结论:
①关于![]() 的一元二次方程
的一元二次方程![]() 的根是
的根是![]() ,3;
,3;
②函数的解析式是![]() ;
;
③![]() ;
;
其中正确的是_______(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() 为小正方形边的中点,
为小正方形边的中点,![]() ,
,![]() 为格点,
为格点,![]() 为
为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
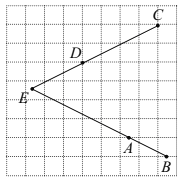
(Ⅰ)![]() 的长等于__________;
的长等于__________;
(Ⅱ)若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出线段
,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
____________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,CD为⊙O的切线,点C是切点.
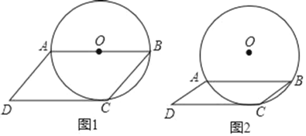
(1)如图1,若AB为⊙O直径,求四边形ABCD各内角的度数;
(2)如图2,若AB为弦,⊙O的半径为3cm,当BC=2cm时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右依次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.
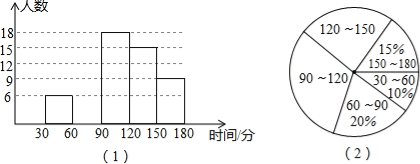
(1)本次调查的学生人数为 人;
(2)补全频数分布直方图;
(3)根据图形提供的信息判断,下列结论正确的是 (只填所有正确结论的代号);
A.由图(1)知,学生完成作业所用时间的中位数在第三组内 |
B.由图(1)知,学生完成作业所用时间的众数在第三组内 |
C.图(2)中,90~120数据组所在扇形的圆心角为108° |
D.图(1)中,落在第五组内数据的频率为0.15 |
(4)学生每天完成作业时间不超过120分钟,视为课业负担适中.根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
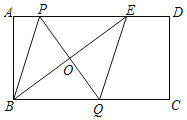
【题目】如图,在矩形ABCD中,E是边AD上一点(不与点A重合),连结BE,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连结BP、EQ.求证:四边形BPEQ是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图,根据信息解答下列问题:

(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图:
(2)求电动汽车一次充电后行驶里程数的中位数、众数:
(3)一次充电后行驶里程数220千米以上(含220千米)为优质等级,若全市有这种电动汽车1200辆,估计优质等级的电动汽车约为多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
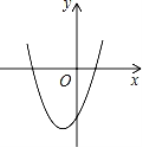
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com