
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
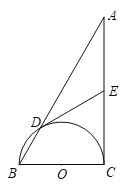
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O的半径为2.
【解析】
(1) 连接OD.通过证明∠ODE=90°,易证得结论;
(2) 由(1)得ED是⊙O的切线;由题意得AC是⊙O的切线,可得ED=EC=EA,又由∠A=30°,在Rt△ABC中,解直角三角形可得BC长,然后半径可得.
(1)证明:连接OD.
∵ ED=EA,
∴ ∠A=∠ADE.
∵ OB=OD,
∴ ∠OBD=∠BDO.
∵ ∠ACB=90°,
∴ ∠A +∠ABC =90°.
∴ ∠ADE +∠BDO =90°.
∴ ∠ODE=90°.
∴ DE是⊙O的切线.
(2)解:∵ ∠ACB =90°, BC为直径,
∴ AC是⊙O的切线.
∵ DE是⊙O的切线,
∴ ED=EC.
∵ ED=![]() ,
,
∴ ED=EC=EA=![]() .
.
∴ AC=![]() .
.
∵ Rt△ABC中∠A=30°,
∴ BC=4.
∴ ⊙O的半径为2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,CD为⊙O的切线,点C是切点.
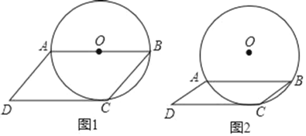
(1)如图1,若AB为⊙O直径,求四边形ABCD各内角的度数;
(2)如图2,若AB为弦,⊙O的半径为3cm,当BC=2cm时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
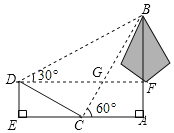
A.20![]() B.30C.30
B.30C.30![]() D.40
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧![]() 的长为
的长为![]() ,直线
,直线![]() 与x轴、y轴分别交于点A、B.
与x轴、y轴分别交于点A、B.
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
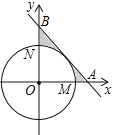
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
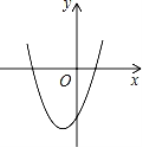
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
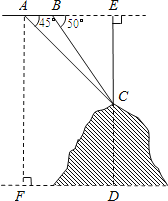
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小辉为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
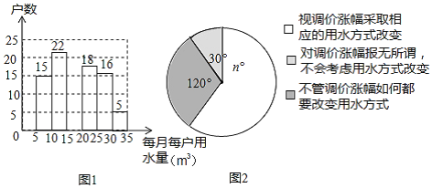
小辉发现每月每户的用水量在![]() 之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小军绘制的图表和发现的信息,完成下列问题:
之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小军绘制的图表和发现的信息,完成下列问题:
(1)![]() ,小明调查了 户居民,并补全图1;
,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数落在 之间,众数落在 之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
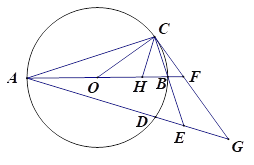
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com