
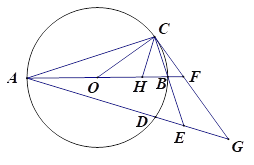
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
【答案】(1)证明见解析;(2)①证明见解析;②5.
【解析】
(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;
(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;
②由△CBH∽△OBC可知:![]() ,所以HB=
,所以HB=![]() ,由于BC=HC,所以OH+HC=4
,由于BC=HC,所以OH+HC=4![]() +BC,利用二次函数的性质即可求出OH+HC的最大值.
+BC,利用二次函数的性质即可求出OH+HC的最大值.
(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线;
(2)①∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC
②由△CBH∽△OBC可知:![]()
∵AB=8,
∴BC2=HBOC=4HB,
∴HB=![]() ,
,
∴OH=OB-HB=4-![]()
∵CB=CH,
∴OH+HC=4![]() +BC,
+BC,
当∠BOC=90°,
此时BC=4![]()
∵∠BOC<90°,
∴0<BC<4![]() ,
,
令BC=x则CH=x,BH=![]()
![]()
当x=2时,
∴OH+HC可取得最大值,最大值为5


科目:初中数学 来源: 题型:
【题目】 如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A是(1,1),点C(a,b),满足![]() .
.
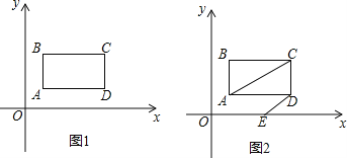
(1)求长方形ABCD的面积;
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发,沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=5时,求三角形OMC的面积;
②若AC∥ED,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
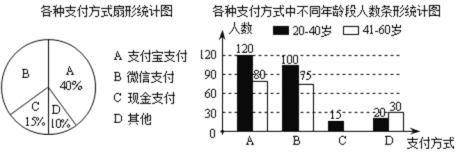
(1)求参与问卷调查的总人数;
(2)补全条形统计图;
(3)该社区参与问卷调查人中,用微信支付方式的哪个年龄段人数多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省城太原某大型超市计划在12月23日推出“十周年”店庆促销活动,该超市为本次促销活动设计了两种促销方案.方案一:全场商品全部打8.5折;方案二:商品总价不超过200元时,不打折,超过200元的部分打7折.小颖的爸爸妈妈准备在该超市促销活动期间去购物.
(1)小颖的爸爸妈妈购买的商品总价为![]() 元(
元(![]() ),按方案一应该支付 元;按方案二应该支付 元;(用含
),按方案一应该支付 元;按方案二应该支付 元;(用含![]() 的代数式表示)
的代数式表示)
(2)若小颖的爸爸妈妈购买的商品总价为300元,请你帮助小颖计算一下,按哪种方案支付更划算;
(3)若小颖的爸爸妈妈购买的商品总价为500元,请你帮助小颖计算一下,按哪种方案支付更划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,AC=6cm ,且BC=4cm,M、N分别是AC、BC的中点,求线段 MN 的的长度.
(2)在(1)中,如果AC=acm,BC=bcm ,其他条件不变,你能猜出MN的长度吗? 如果可以,请证明你所得出的结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
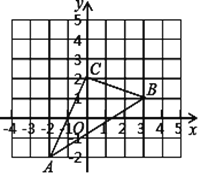
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小聪将三角尺Rt△ABC绕点C逆时针方向旋转到△DEC的位置,其中∠A为30°,∠B为直角,若点A、C、E在一条直线上,则此次旋转变换中旋转角的度数为____.
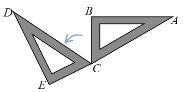
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,作射线
的中点,作射线![]() ,连接
,连接![]() .
.
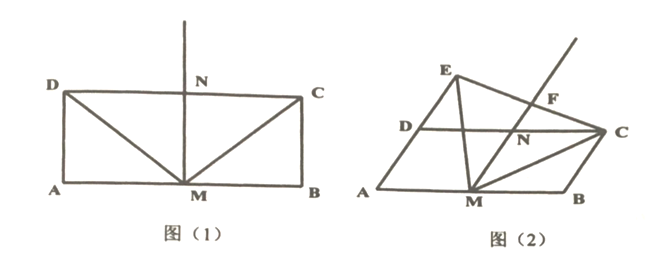
(1)请直接写出线段![]() 与
与![]() 的数量关系;
的数量关系;
(2)将矩形![]() 变为平行四边形,其中
变为平行四边形,其中![]() 为锐角,如图(2),
为锐角,如图(2),![]() ,
,![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)写出![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com