
【题目】 如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A是(1,1),点C(a,b),满足![]() .
.
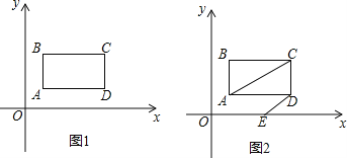
(1)求长方形ABCD的面积;
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发,沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=5时,求三角形OMC的面积;
②若AC∥ED,求t的值.
【答案】(1)8;(2)①4;②3
【解析】
(1)由已知得出a=5,b=3,求得C点坐标,结合图象,能找出其它几点的坐标,从而能得出长方形ABCD的面积;
(2)①拆分三角形,求出各个图形的面积即可求得;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,根据平行四边形的性质可得出AF的长度,结合AM的长度可得出ME为△FAD的中位线,根据点M、A的运动速度可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵![]() .
.
∴a-5=0,b-3=0,即a=5,b=3,
∵四边形ABCD为长方形,
∴点B(1,3),点C(5,3),点D(5,1),
∴AB=3-1=2,BC=5-1=4,
长方形ABCD的面积为:AB×BC=2×4=8;
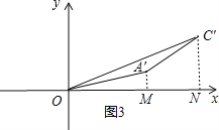
(2)①将t=5时,线段AC拿出来,放在图3中,各字母如图,
∵点A′(6,1),点C′(10,3),
∴OM=6,ON=10,A′M=1,C′N=3,MN=ON-OM=4,
∴三角形OA′C′的面积=![]() ONC′N-
ONC′N-![]() OMA′M-
OMA′M-![]() (A′M+C′N)MN=15-3-8=4;
(A′M+C′N)MN=15-3-8=4;
即三角形OMC的面积为4;
②过点A作AF∥CD,交x轴于点M,交DE的延长线于点F,
如图4所示,
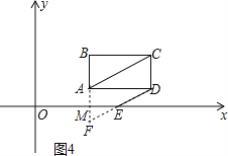
∵AF∥CD,AC∥DF,
∴四边形AFDC为平行四边形,
∴AF=CD=2.
∵AM=1,
∴ME为△FAD的中位线,
∴ME=![]() AD=2,
AD=2,
即2t-(t+1)=2,
解得:t=3.
故若AC∥ED,t的值为3秒.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 从原点出发沿数轴向左运动,同时点
从原点出发沿数轴向左运动,同时点![]() 从原点出发沿数轴向右运动,
从原点出发沿数轴向右运动,![]() 秒钟后,两点相距
秒钟后,两点相距![]() 个单位长度,已知点
个单位长度,已知点![]() 的速度是点A的速度的
的速度是点A的速度的![]() 倍.(速度单位:单位长度/秒)
倍.(速度单位:单位长度/秒)
![]()
(1)求出点![]() 点
点![]() 运动的速度.
运动的速度.
(2)若![]() 、
、![]() 两点从(1)中位置开始,仍以原来的速度同时沿数轴向左运动,几秒时原点恰好处在点
两点从(1)中位置开始,仍以原来的速度同时沿数轴向左运动,几秒时原点恰好处在点![]() 点
点![]() 的正中间?
的正中间?
(3)若![]() 、
、![]() 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点
两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点![]() 同时从
同时从![]() 点位置出发向
点位置出发向![]() 点运动,当遇到
点运动,当遇到![]() 点后,立即返回向
点后,立即返回向![]() 点运动,遇到
点运动,遇到![]() 点又立即返回向
点又立即返回向![]() 点运动,如此往返,直到
点运动,如此往返,直到![]() 点追上
点追上![]() 点时,点
点时,点![]() 一直以
一直以![]() 单位长度/秒的速度运动,那么点
单位长度/秒的速度运动,那么点![]() 从开始运动到停止运动,行驶的路程是多少单位长度.
从开始运动到停止运动,行驶的路程是多少单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:![]() 分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:
分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:![]() 经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
(1)当点C的坐标为![]() 时,①求直线l2的函数表达式;②求证:AE平分
时,①求直线l2的函数表达式;②求证:AE平分![]() ;
;
(2)问:是否存在点C,使![]() 是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
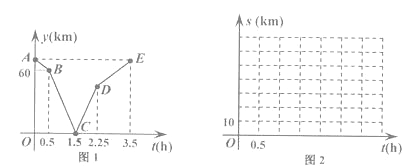
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
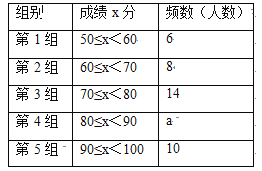
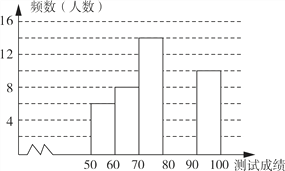
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a a3a5
(2)(x6)2+(x3)4+x12
(3)![]()
![]()
(4)(-3a2b3)(-2ab3c)3
(5)![]()
(6)(x+2)(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
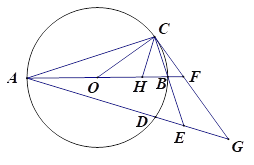
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com