【题目】如图，点
从原点出发沿数轴向左运动，同时点
从原点出发沿数轴向右运动，
秒钟后，两点相距
个单位长度，已知点的速度是点A的速度的
倍．（速度单位：单位长度/秒）
（1）求出点点运动的速度．
（2）若、两点从（1）中位置开始，仍以原来的速度同时沿数轴向左运动，几秒时原点恰好处在点点的正中间?
（3）若、两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点
同时从点位置出发向点运动，当遇到点后，立即返回向点运动，遇到点又立即返回向点运动，如此往返，直到点追上点时，点一直以
单位长度/秒的速度运动，那么点从开始运动到停止运动，行驶的路程是多少单位长度．
【答案】（1）
、
这动的速度分别为
单位长度/秒，
单位长度/秒；（2）
秒时，原点给好处在点点正中间；（3）
行驶的路程是
个单位长度．
【解析】
（1）设点A的速度为每秒x个单位，则点B的速度为每秒3x个单位，由甲的路程＋乙的路程＝总路程建立方程求出其解即可；
（2）设t秒时原点恰好在A、B的中间，根据两点离原点的距离相等建立方程求出其解即可；
（3）先根据追击问题求出A、B相遇的时间就可以求出C行驶的路程．
（1）设点A的速度为每秒x个单位，则点B的速度为每秒3x个单位，
由题意，得
4x＋4×3x＝16，
解得：x＝1，
所以点A的速度为每秒单位长度/秒，则点B的速度为单位长度/秒．
（2）设
秒后原点位于、点正中间．
秒时，原点给好处在点点正中间．
（3）设点追上点的时间为
秒
（秒）
点行驶路程：
（单位长度）
行驶的路程是个单位长度．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案科目：初中数学 来源： 题型：
【题目】如图，直线l1∥l2∥l3，等腰直角三角形ABC的三个顶点A，B，C分别在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离为1，l2与l3的距离为3，则
的值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM.
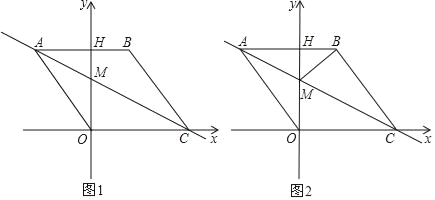
（1）菱形ABCO的边长
（2）求直线AC的解析式；
（3）动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，
①当0＜t＜
时，求S与t之间的函数关系式；
②在点P运动过程中，当S=3，请直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l1：y=kx+b经过点A（5，0），B（1，4）．
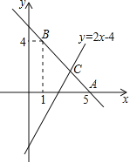
（1）求直线AB的函数关系式；
（2）若直线l2：y=2x-4与直线AB相交于点C，求点C的坐标；
（3）过点P(m,0)作x轴的垂线，分别交直线点l1，l2与点M，N，若m>3, 当MN=3时，求m 的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
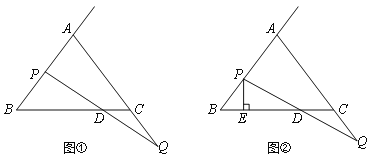
【题目】已知△ABC中，AB＝AC＝BC＝6．点P射线BA上一点，点Q是AC的延长线上一点，且BP＝CQ，连接PQ，与直线BC相交于点D．
（1）如图①，当点P为AB的中点时，求CD的长；
（2）如图②，过点P作直线BC的垂线，垂足为E，当点P，Q分别在射线BA和AC的延长线上任意地移动过程中，线段BE，DE，CD中是否存在长度保持不变的线段？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的三分线，在△ABC中，∠B＝30°，AD和 DE是△ABC的三分线，点D在 BC 边上，点E在 AC边上，且AD＝BD，DE＝CE，请写出∠C所有可能的度数________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，然后解决问题：和、差、倍、分等问题中有着广泛的应用，截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．
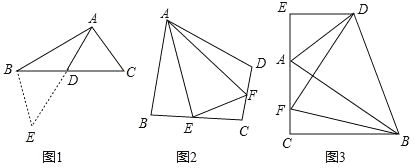
（1）如图1，在△ABC中，若 AB＝12，AC＝8，求 BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使 DE＝AD，再连接 BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决：
（2）如图2，在四边形ABCD中，AB＝AD，∠ABC+∠ADC＝180°，E、F分别是边BC，CD上的两点，且∠EAF＝
∠BAD，求证：BE+DF＝EF．
问题拓展：
（3）如图3，在△ABC中，∠ACB＝90°，∠CAB＝60°，点D是△ABC 外角平分线上一点，DE⊥AC交 CA延长线于点E，F是 AC上一点，且DF＝DB．
求证：AC﹣AE＝AF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明同学在学习整式时发现，如果合理地使用乘法公式可以简化运算，于是在解此道计算题时他是这样做的（如下）：
第一步
第二步
小华看到小明的做法后，对他说：“你做错了，在第一步运用公式时出现了错误，你好好检查一下．”小明认真仔细检查后，自己发现了一处错误圈画了出来，并进行了纠正（如下）：
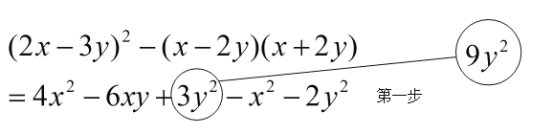
小华看到小明的改错后说：“你还有错没有改出来．”
（1）你认为小华说的对吗？_________（填“对”或“不对”）；
（2）如果小华说的对，那么小明还有哪些错误没有找出来，请你帮助小明把第一步中的其它错误圈画出来并改正，然后写出此题的正确解题过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图1，在平面直角坐标系中，第一象限内长方形ABCD，AB∥y轴，点A是（1，1），点C（a，b），满足
．
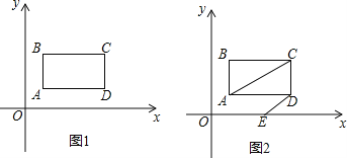
（1）求长方形ABCD的面积；
（2）如图2，长方形ABCD以每秒1个单位长度的速度向右平移，同时点E从原点O出发，沿x轴以每秒2个单位长度的速度向右运动，设运动时间为t秒．
①当t=5时，求三角形OMC的面积；
②若AC∥ED，求t的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com