
【题目】如图(1),在矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,作射线
的中点,作射线![]() ,连接
,连接![]() .
.
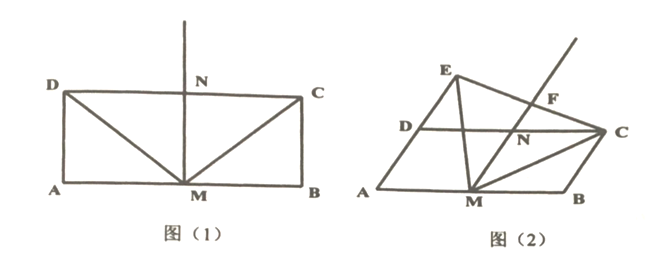
(1)请直接写出线段![]() 与
与![]() 的数量关系;
的数量关系;
(2)将矩形![]() 变为平行四边形,其中
变为平行四边形,其中![]() 为锐角,如图(2),
为锐角,如图(2),![]() ,
,![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)写出![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【答案】(1)MD=MC;(2)见解析;(3)∠BME=3∠AEM,证明见解析.
【解析】
(1)由“SAS”可证△ADM≌△BCM,可得MD=MC;
(2)由题意可证四边形ADNM是平行四边形,可得AD∥MN,可得EF=FC,MF⊥EC,由线段垂直平分线的性质可得ME=MC;
(3)由等腰三角形的性质和平行线的性质可得∠BME=3∠AEM.
解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,
∵点M是AB中点,
∴AM=BM,
∴△ADM≌△BCM(SAS),
∴MD=MC;
(2)∵M、N分别是AB、CD的中点,
∴AM=BM,CN=DN,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DN=AM=CN=BM,
∴四边形ADNM是平行四边形,
∴AD∥MN,
∴![]() ,∠AEC=∠NFC=90°,
,∠AEC=∠NFC=90°,
∴EF=CF,且MF⊥EC,
∴ME=MC;
(3)∠BME=3∠AEM,
证明:∵EM=MC,EF=FC,
∴∠EMF=∠FMC,
∵AB=2BC,M是AB中点,
∴MB=BC,
∴∠BMC=∠BCM,
∵MN∥AD,AD∥BC,
∴AD∥MN∥BC,
∴∠AEM=∠EMF,∠FMC=∠BCM,
∴∠AEM=∠EMF=∠FMC=∠BCM=∠BMC,
∴∠BME=3∠AEM.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
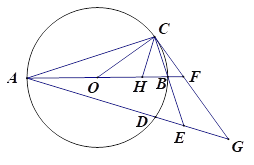
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
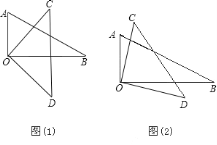
【题目】把一副三角板的直角顶点O重叠在一起,
(1)如图(1),当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
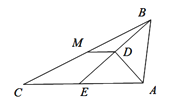
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
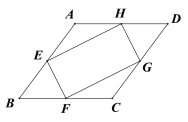
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表

(1)此表反映的是变量 随 变化的情况.
(2)请直接写出y与x的关系式为 .
(3)当气温为22℃时,某人看到烟花燃放5秒后才听到声响,求此人与烟花燃放所在地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90![]() ,∠ACB=30
,∠ACB=30![]() ,AB=2,AD=2AC,DC=2BC.
,AB=2,AD=2AC,DC=2BC.
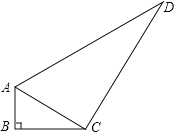
(1)求证:△ACD为直角三角形;(2)求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com