
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
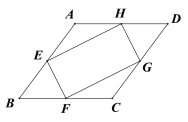
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
科目:初中数学 来源: 题型:
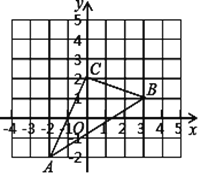
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
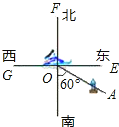
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() 分别是
分别是![]() 的中点,作射线
的中点,作射线![]() ,连接
,连接![]() .
.
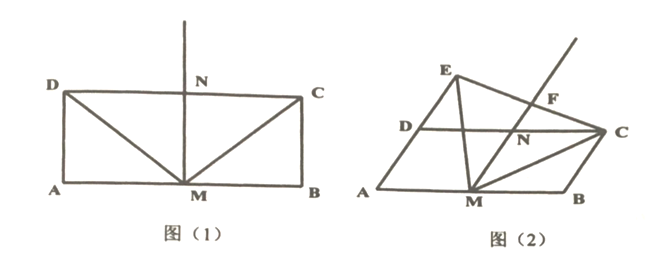
(1)请直接写出线段![]() 与
与![]() 的数量关系;
的数量关系;
(2)将矩形![]() 变为平行四边形,其中
变为平行四边形,其中![]() 为锐角,如图(2),
为锐角,如图(2),![]() ,
,![]() 分别是
分别是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)写出![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表

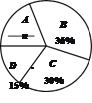
依据以上统计信息,解答下列问题:
(1)求得m= ,n= ;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在纸面上有一数轴如图所示.

尝试:折叠纸面,使表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示_________的点重合.
的点与表示_________的点重合.
发现:折叠纸面,使表示![]() 的点与表示3的点重合,则表示5的点与表示____________的点重合.
的点与表示3的点重合,则表示5的点与表示____________的点重合.
应用:若数轴上![]() 、
、![]() 两点之间的距离为11(
两点之间的距离为11(![]() 在
在![]() 左侧),且经过折叠后,表示
左侧),且经过折叠后,表示![]() 的点与表示3的点重合,点
的点与表示3的点重合,点![]() 与点
与点![]() 重合,分别求
重合,分别求![]() 、
、![]() 两点表示的数.
两点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为________.
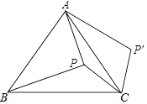
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图![]() 可以得到
可以得到![]() ,基于此,请解答下列问题:
,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,![]() = .
= .
(3) 小明同学用图 中x 张边长为a 的正方形, y张边长为b 的正方形,z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形,则x+y+z=
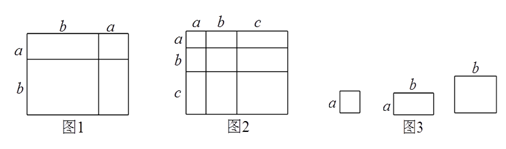
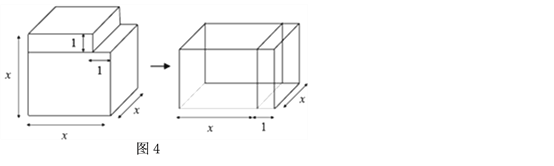
【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为![]() 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com