练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠1＝80°，∠2＝100°，∠C＝∠D．

    （1）判断AC与DF的位置关系，并说明理由；

    （2）若∠C比∠A大20°，求∠F的度数．

    【答案】（1）AC∥DF，理由见解析；（2）40°．

    【解析】

    （1）根据平行线的性质得出∠ABD＝∠C，求出∠D＝∠ABD，根据平行线的判定得出AC∥DF；

    （2）根据平行线的性质和三角形内角和解答即可；

    解：（1）AC∥DF，理由如下：

    ∵∠1＝80°，∠2＝100°，

    ∴∠1+∠2＝180°，

    ∴BD∥CE，

    ∴∠ABD＝∠C，

    ∵∠C＝∠D，

    ∴∠ABD＝∠D，

    ∴AC∥DF；

    （2）∵AC∥DF，

    ∴∠A＝∠F，∠ABD＝∠D，

    ∵∠C＝∠D，∠1＝80°，

    ∴∠A+∠ABD＝180°﹣80°＝100°，

    即∠A+∠C＝100°，

    ∵∠C比∠A大20°，

    ∴∠A＝40°，

    ∴∠F＝40°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某集团购买了150吨物资打算运往某地支援，现有甲、乙、丙三种车型供选择，每辆汽车的运载能力和运费如下表所示：（假设每辆车均满载）

    车型

    甲

    乙

    丙

    汽车运载量（吨/辆）

    5

    8

    10

    汽车运费（元/辆）

    1000

    1200

    1500

    （1）若全部物资都用甲、乙两种车型来运送，需运费24000元，问分别需甲、乙两种车型各多少辆？

    （2）若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送，请你写出可能的运送方案，并帮助该集团找出运费最省的方案（甲、乙、丙三种车辆均要参与运送）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有一项工程，甲单独做需要10天能完成，乙单独做需要15天能完成，甲做一天需要的报酬比乙做一天需要的报酬多100元，甲、乙合作完成此项工程需要5400元报酬．

    （1）问甲、乙合作多少天能完成此项工程？

    （2）求甲做一天需要的报酬；

    （3）为了节省开支，应在甲单独完成、乙单独完成、甲乙合作完成这三种方案中选择哪种方案？请通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两条宽度都为1的纸条，交叉重叠放在一起，且它们的交角为α，则它们重叠部分（图中阴影部分）的面积为（ ）

    A.
    B.
    C.sinα
    D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，且交AD于点E，交BC于点F，连接BE，DF，且BE平分∠ABD．

    ①求证：四边形BFDE是菱形；

    ②直接写出∠EBF的度数．

    （2）把（1）中菱形BFDE进行分离研究，如图2，G，I分别在BF，BE边上，且BG＝BI，连接GD，H为GD的中点，连接FH，并延长FH交ED于点J，连接IJ，IH，IF，IG．试探究线段IH与FH之间满足的关系，并说明理由；

    （3）把（1）中矩形ABCD进行特殊化探究，如图3，矩形ABCD满足AB＝AD时，点E是对角线AC上一点，连接DE，作EF⊥DE，垂足为点E，交AB于点F，连接DF，交AC于点G．请直接写出线段AG，GE，EC三者之间满足的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们在过去的学习中已经发现了如下的运算规律：

    (1)15×15＝1×2×100＋25＝225；

    (2)25×25＝2×3×100＋25＝625；

    (3)35×35＝3×4×100＋25＝1225；

    ……

    按照这种规律，第n个式子可以表示为

    A. n×n＝×(＋1)×100＋25＝n2

    B. n×n＝×(＋1)×100＋25＝n2

    C. (n＋5)×(n＋5)＝n×(n＋1)×100＋25＝n2＋10n＋25

    D. (10n＋5)×(10n＋5)＝n×(n＋l)×l00＋25＝100n2＋100n＋25

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P．OF∥BC交AC于点E，交PC于点F，连结AF．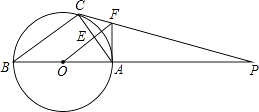

    （1）判断AF与⊙O的位置关系并说明理由；
    （2）已知半径为20，AF=15，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（π﹣4）0+|3﹣tan60°|﹣（ ）﹣2+ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在等腰△ABC 中，AB=AC=10，BC=16．

    （1）若将△ABC 的腰不变，底变为 12，甲同学说，这两个等腰三角形面积相等；乙同学说，腰不变，底变化，这两个三角形面积必不相等，请对甲、乙两种说法做出判断，并说明理由；

    （2）已知△ABC 底边上高增加 x，腰长增加（x﹣2）时，底却保持不变，请确定 x 的值．

    查看答案和解析>>

    同步练习册答案