
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

【答案】(1)①详见解析;②60°.(2)IH=![]() FH;(3)EG2=AG2+CE2.
FH;(3)EG2=AG2+CE2.
【解析】
(1)①由△DOE≌△BOF,推出EO=OF,∵OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可.
②先证明∠ABD=2∠ADB,推出∠ADB=30°,延长即可解决问题.
(2)IH=![]() FH.只要证明△IJF是等边三角形即可.
FH.只要证明△IJF是等边三角形即可.
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
(1)①证明:如图1中,
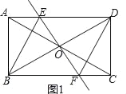
∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
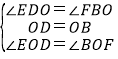 ,
,
∴△DOE≌△BOF,
∴EO=OF,∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,OB=OD,
∴EB=ED,
∴四边形EBFD是菱形.
②∵BE平分∠ABD,
∴∠ABE=∠EBD,
∵EB=ED,
∴∠EBD=∠EDB,
∴∠ABD=2∠ADB,
∵∠ABD+∠ADB=90°,
∴∠ADB=30°,∠ABD=60°,
∴∠ABE=∠EBO=∠OBF=30°,
∴∠EBF=60°.
(2)结论:IH=![]() FH.
FH.
理由:如图2中,延长BE到M,使得EM=EJ,连接MJ.
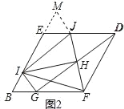
∵四边形EBFD是菱形,∠B=60°,
∴EB=BF=ED,DE∥BF,
∴∠JDH=∠FGH,
在△DHJ和△GHF中,
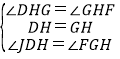 ,
,
∴△DHJ≌△GHF,
∴DJ=FG,JH=HF,
∴EJ=BG=EM=BI,
∴BE=IM=BF,
∵∠MEJ=∠B=60°,
∴△MEJ是等边三角形,
∴MJ=EM=NI,∠M=∠B=60°
在△BIF和△MJI中,
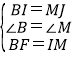 ,
,
∴△BIF≌△MJI,
∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,
∴IH⊥JF,
∵∠BFI+∠BIF=120°,
∴∠MIJ+∠BIF=120°,
∴∠JIF=60°,
∴△JIF是等边三角形,
在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,
∴∠FIH=30°,
∴IH=![]() FH.
FH.
(3)结论:EG2=AG2+CE2.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,
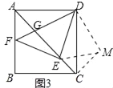
∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
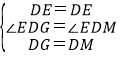 ,
,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.


科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
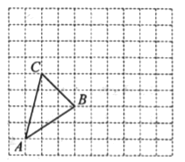
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )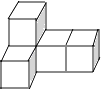
A.主视图的面积最小
B.左视图的面积最小
C.俯视图的面积最
D.三个视图的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
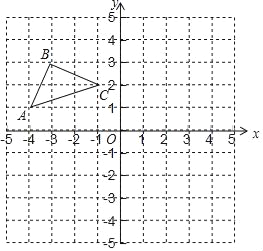
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.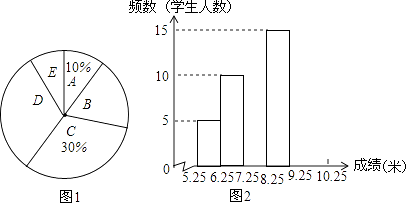
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
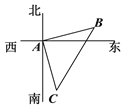
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com