练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】省城太原某大型超市计划在12月23日推出“十周年”店庆促销活动，该超市为本次促销活动设计了两种促销方案．方案一：全场商品全部打8.5折；方案二：商品总价不超过200元时，不打折，超过200元的部分打7折．小颖的爸爸妈妈准备在该超市促销活动期间去购物．

    （1）小颖的爸爸妈妈购买的商品总价为元()，按方案一应该支付 元；按方案二应该支付 元；（用含的代数式表示）

    （2）若小颖的爸爸妈妈购买的商品总价为300元，请你帮助小颖计算一下，按哪种方案支付更划算；

    （3）若小颖的爸爸妈妈购买的商品总价为500元，请你帮助小颖计算一下，按哪种方案支付更划算．

    【答案】（1），；（2）按方案一支付更划算，见解析；（3）按方案二支付更划算，见解析

    【解析】

    （1）方案一全场商品全部打8.5折，原价乘以折扣即可；方案二分段计算，不打折部分200元，打折部分元，打7折后为元，两部分相加化简即可.

    （2）将元分别代入第（1）得到的两个代数式求值比较即可.

    （3）将元分别代入第（1）得到的两个代数式求值比较即可.

    解：（1），

    .

    （2）当小颖的爸爸妈妈购买的商品总价为300元时，

    按方案一需支付： (元).

    按方案二需支付： (元).

    ，

    ∴按方案一支付更划算.

    （3）当小颖的爸爸妈妈购买的商品总价为500元时，

    按方案一需支付： (元).

    按方案二需支付： (元).

    ，

    ∴按方案二支付更划算.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲骑自行车从M地出发沿一条公路匀速前往N地，乙骑摩托车从N地出发沿同一条公路匀速前往M地，

    已知乙比甲晚出发0.5小时且先到达目的地．设甲行驶的时间为t(h)，甲乙两人之间的路程为y(km)，

    y与t的函数关系如图1所示，请解决以下问题：

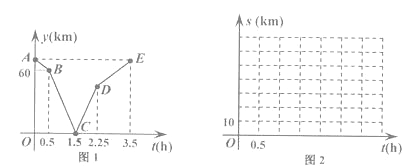
    （1）写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式．

    （2）①求点D的纵坐标．

    ②求M，N两地之间的距离．

    （3）设乙离M地的路程为S乙 (km)，请直接写出S甲 与时间t(h)的函数表达式，并在图2所给的直角坐标系中画出它的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算:

    （1）a a3a5

    （2）（x6）2+（x3）4+x12

    （3）

    （4）(-3a2b3)(-2ab3c)3

    （5）

    （6）(x+2)(x-3)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：Rt△ABC 中，AC＝BC，∠ACB＝90°，D 为 BC 边中点，CF⊥AD 交 AD 于 E，交 AB 于 F，BE交 AC 于 G，连 DF，下列结论：①AC＝AF，②CD＋DF＝AD，③∠ADC＝∠BDF，④CE＝BE，⑤∠ BED＝45°，其中正确的有（ ）

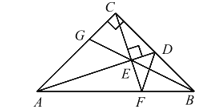
    A. 5 个B. 4 个C. 3 个D. 2 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E，F分别为边AB，CD的中点，BD是对角线．

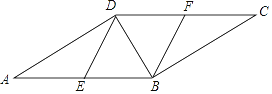
    （1）求证：△ADE≌△CBF；

    （2）若∠ADB是直角，请证明四边形BEDF是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践：某“综合与实践”小组开展了“正方体纸盒的制作”实践活动，他们利用长为，宽为长方形纸板制作出两种不同方案的正方体盒子， 请你动手操作验证并完成任务．(纸板厚度及接缝处忽略不计)

    动手操作一：

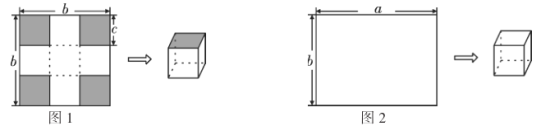
    如图1，若，按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来就可以做成一个无盖的正方体纸盒．

    问题解决：（1）此时，你发现与之间存在的数量关系为 ．

    动手操作二：

    如图2，若，现在在纸板的四角剪去两个小正方形和两个小长方形恰好可以制作成一个有盖的正方体纸盒，其大小与（1）中无盖正方体大小一样．

    拓展延伸：（2）请你在图2中画出你剪去的两个小正方形和两个小长方形(用阴影表示)，折痕用虚线表示；

    （3）此时，你发现与之间存在的数量关系为 ；若，求有盖正方体纸盒的表面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

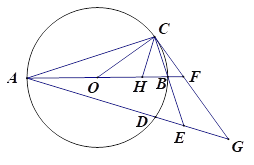
    【题目】如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE

    （1）求证：直线CG为⊙O的切线；

    （2）若点H为线段OB上一点，连接CH，满足CB＝CH，

    ①△CBH∽△OBC

    ②求OH＋HC的最大值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，OA＝3，OC＝2，F是AB上的一个动点(F不与A，B重合)，过点F的反比例函数y＝ (x＞0)的图象与BC边交于点E.

    (1)当F为AB的中点时，求该函数的解析式；

    (2)当k为何值时，△EFA的面积最大，最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

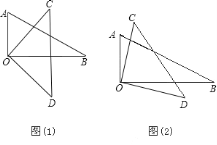
    【题目】把一副三角板的直角顶点O重叠在一起，

    （1）如图（1），当OB平分∠COD时，则∠AOD和∠BOC的和是多少度？

    （2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？

    查看答案和解析>>

    同步练习册答案