
【题目】(1)如图,已知点C在线段AB上,AC=6cm ,且BC=4cm,M、N分别是AC、BC的中点,求线段 MN 的的长度.
(2)在(1)中,如果AC=acm,BC=bcm ,其他条件不变,你能猜出MN的长度吗? 如果可以,请证明你所得出的结论.
![]()
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
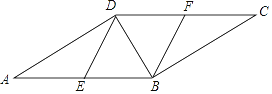
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
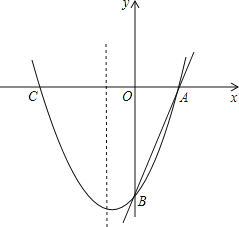
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
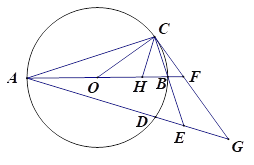
【题目】如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
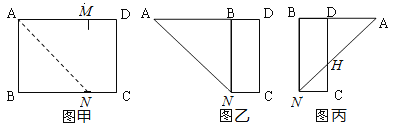
【题目】如图甲,ABCD是一矩形纸片,AB=3cm,AD=4cm,M是AD上一点,且AM=3cm.操作:
(1)将AB向AM折过去,使AB与AM重合,得折痕AN,如图乙;
(2)将△ANB以BN为折痕向右折过去,得图丙.
则HD是( )cm
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
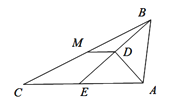
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com