
分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{(x-1)^{2}}{x-1}$-$\frac{\sqrt{(x-2)^{2}}}{x(x-2)}$
=x-1-$\frac{|x-2|}{x(x-2)}$,
当a=2-$\sqrt{2}$时,原式=2-$\sqrt{2}$-1-$\frac{|2-\sqrt{2}-2|}{(2-\sqrt{2})(2-\sqrt{2}-2)}$=1-$\sqrt{2}$-$\frac{\sqrt{2}}{-\sqrt{2}(2-\sqrt{2})}$=2-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
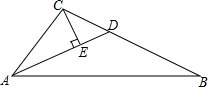 如图,已知△ABC,AD平分∠BAC,∠CAB=2∠B,CE⊥AD于E,且CB=10.(1)求AE的长;
如图,已知△ABC,AD平分∠BAC,∠CAB=2∠B,CE⊥AD于E,且CB=10.(1)求AE的长;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.79×103 | B. | 3.79×104 | C. | 3.79×105 | D. | 0.379×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
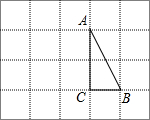 如图,在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个整数 | |
| B. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的平方 | |
| C. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的立方 | |
| D. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的四次方 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.375 | B. | 0.6 | C. | 15 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com