
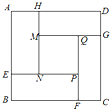
【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢,设计图案如图所示(四周是四个全等的矩形,用材料甲进行装潢;中心区是正方形MNPQ,用材料乙进行装潢).
两种装潢材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,装潢材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1760元购买材料一定够用吗?请说明理由.
【答案】(1)(6﹣2x);(2)y=﹣40x2+240x+1440;(3)预备资金1760元购买材料一定够用,理由见解析
【解析】
(1)根据大正方形的边长减去两个小长方形的宽即可求解;
(2)根据总费用等于两种材料的费用之和即可求解;
(3)利用二次函数的性质和最值解答即可.
解:(1)∵AH=GQ=x,AD=6,
∴MQ=6-2x;
故答案为:6-2x;
(2)根据题意,得AH=x,AE=6﹣x, S甲=4S长方形AENH=4x(6﹣x)=24x﹣4x2,
S乙=S正方形MNQP=(6﹣2x)2=36﹣24x+4x2.
∴ y=50(24x﹣4x2)+40(36﹣24x+4x2)=﹣40x2+240x+1440.
答:y关于x的函数解析式为y=﹣40x2+240x+1440.
(3)预备资金1760元购买材料一定够用.理由如下:
∵y=﹣40x2+240x+1440=﹣40(x-3)2+1800,
由﹣40<0,可知抛物线开口向下,在对称轴的左侧,y随x的增大而增大.
由x-3=0可知,抛物线的对称轴为直线x=3.
∴ 当x<3时,y随x的增大而增大.
∵ 中心区的边长不小于2米,即6﹣2x≥2,解得x≤2,又x>0,∴0<x≤2.
当x=2时,y=﹣40(x-3)2+1800=﹣40(2-3)2+1800=1760,
∴ 当0<x≤2时,y≤1760.
∴ 预备资金1760元购买材料一定够用.
答:预备资金1760元购买材料一定够用.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,面积为150.
,面积为150.

(1)尺规作图:作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(不要求写作法,保留作图痕迹)
;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求出点![]() 到两条直角边的距离.
到两条直角边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系中, △ABC的顶点坐标分别为A(2,0),B(3,2),C(5,-2). 以原点O为位似中心,在y轴的右侧将△ABC放大为原来的两倍得到△![]() .
.
(1)画出△![]() ;
;
(2)分别写出B, C两点的对应点![]() ,
, ![]() 的坐标.
的坐标.
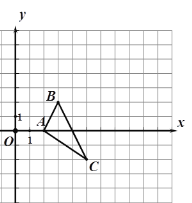
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 对于平面直角坐标系xOy上的点P(a, b) 和抛物线![]() , 我们称P(a, b)是抛物线
, 我们称P(a, b)是抛物线![]() 的相伴点, 抛物线
的相伴点, 抛物线![]() 是点P(a, b) 的相伴抛物线.
是点P(a, b) 的相伴抛物线.
如图,已知点A(-2, -2),B(4, -2),C(1, 4).
(1) 点A的相伴抛物线的解析式为 ;过A, B两点的抛物线![]() 的相伴点坐标为 ;
的相伴点坐标为 ;
(2) 设点P(a, b) 在直线AC上运动:
①点P(a, b)的相伴抛物线的顶点都在同一条抛物线Ω上, 求抛物线Ω的解析式.
②当点P(a, b)的相伴抛物线的顶点落在△ABC 内部时, 请直接写出 a 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
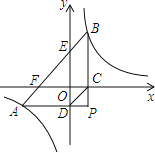
【题目】如图,![]() 的直角顶点P在第四象限,顶点A、B分别落在反比例函数
的直角顶点P在第四象限,顶点A、B分别落在反比例函数![]() 图象的两支上,且
图象的两支上,且![]() 轴于点C,
轴于点C,![]() 轴于点D,AB分别与x轴,y轴相交于点F和
轴于点D,AB分别与x轴,y轴相交于点F和![]() 已知点B的坐标为
已知点B的坐标为![]() .
.
![]() 填空:
填空:![]() ______;
______;
![]() 证明:
证明:![]() ;
;
![]() 当四边形ABCD的面积和
当四边形ABCD的面积和![]() 的面积相等时,求点P的坐标.
的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
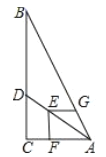
【题目】如图,在 RtABC 中, ACB 90 , AC 6 , BC 12 ,点 D 在边 BC 上,点 E在线段 AD 上, EF AC 于点 F , EG EF 交 AB 于点 G .若 EF EG ,则 CD 的长为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
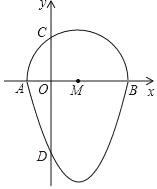
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com