【题目】如图, 在平面直角坐标系中, △ABC的顶点坐标分别为A（2，0），B（3，2），C（5，-2）． 以原点O为位似中心，在y轴的右侧将△ABC放大为原来的两倍得到△
．
（1）画出△；
（2）分别写出B, C两点的对应点
, 
的坐标．
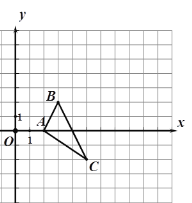
科目：初中数学 来源： 题型：
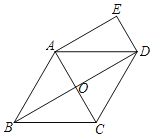
【题目】已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB＝2，∠BCD＝120°，求四边形AODE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC不动，△ADE绕点A旋转，连接BE，CD，F为BE的中点，连接AF.
(1)如图①，当∠BAE＝90°时，求证：CD＝2AF；
(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
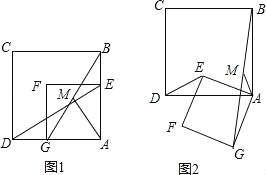
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形．
（1）如图1，连接DE，BG，M为线段BG的中点，连接AM，探究AM与DE的数量关系和位置关系，并证明你的结论；
（2）在图1的基础上，将正方形AEFG绕点A逆时针方向旋转到图2的位置，连结DE、BG，M为线段BG的中点，连结AM，探究AM与DE的数量关系和位置关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，点
，将点A向右平移6个单位长度，得到点B.
(1)直接写出点B的坐标；
(2)若抛物线y=-x2+bx+c经过点A,B，求抛物线的表达式；
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动，当抛物线与线段AB有且只有一个公共点时，求抛物线顶点横坐标
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
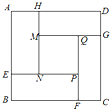
【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢，设计图案如图所示（四周是四个全等的矩形，用材料甲进行装潢；中心区是正方形MNPQ，用材料乙进行装潢）．
两种装潢材料的成本如下表：
材料 | 甲 | 乙 |
价格（元/米2） | 50 | 40 |
设矩形的较短边AH的长为x米，装潢材料的总费用为y元．
（1）MQ的长为 米（用含x的代数式表示）；
（2）求y关于x的函数解析式；
（3）当中心区的边长不小于2米时，预备资金1760元购买材料一定够用吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，A（4，0），B（0，3），C（4，3），I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I'的坐标为（ ）
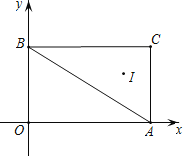
A. （﹣2，3） B. （﹣3，2） C. （3，﹣2） D. （2，﹣3）
查看答案和解析>>
科目：初中数学 来源： 题型：
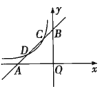
【题目】如图，已知直线
与x轴、y轴分别交于点A，B，与双曲线
分别交于点C，D，且点C的坐标为
.
（1）分别求出直线、双曲线的函数表达式.
（2）求出点D的坐标.
（3）利用图象直接写出：当x在什么范围内取值时
？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
