
【题目】雅安地震,牵动着全国人民的心,地震后某中学举行了爱心捐款活动,图是根据该校九年级某班学生为雅安灾区捐款情况绘制的不完整的条形统计图和扇形统计图.

(1)求该班学生总人数;
(2)补全条形统计图;
(3)若该校九年级有800人,据此样本,请你估计该校九年级学生共捐款多少元.
科目:初中数学 来源: 题型:
【题目】扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步,分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步,从左边一堆拿出两张,放入中间一堆;
第三步,从右边一堆拿出一张,放入中间一堆;
第四步,左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数,聪明的你,你认为中间一堆牌的张数是多少?
【答案】5
【解析】
此题看似复杂,其实只是考查了整式的基本运算.把每堆牌的数量用相应的字母表示出来,列式表示变化情况即可找出最后答案.
解答:解:设第一步时候,每堆牌的数量都是x(x≥2);
第二步时候:左边x-2,中间x+2,右边x;
第三步时候:左边x-2,中级x+3,右边x-1;
第四步开始时候,左边有(x-2)张牌,则从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5.
所以中间一堆牌此时有5张牌.
【题型】填空题
【结束】
44
【题目】为什么总是1 089?
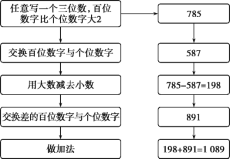
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y= ![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1). 
(1)求一次函数和反比例函数的解析式;
(2)求点C的坐标;
(3)结合图象直接写出不等式0<x+m≤ ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且 ![]() =
= ![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F. 
(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为8×8的正方形网格,请在所给的网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A坐标为(﹣2,4),点B坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则写出点C的坐标,写出△ABC的周长(结果保留根号);
(3)画出△ABC关于y轴的对称图形△A1B1C1;并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=20cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点

(1)若点C恰好是AB中点,则DE的长是多少?(直接写出结果)
(2)若BC=14cm,求DE的长
(3)试说明不论BC取何值(不超过20cm),DE的长不变
(4)知识迁移:如图②,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试求出∠DOE的大小,并说明∠DOE的大小与射线OC的位置是否有关?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com