
����Ŀ����ͼ�ǹ��Ϊ8��8���������������������������а�����Ҫ�������
��1�����������н���ƽ��ֱ������ϵ��ʹ��A����Ϊ����2��4������B����Ϊ����4��2����
��2���ڵڶ������ڵĸ���ϻ�һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������д����C�����꣬д����ABC���ܳ�������������ţ���
��3��������ABC����y��ĶԳ�ͼ����A1B1C1����д����A1��B1��C1�����꣮

���𰸡���1������������2��![]() ����3��A1��2��4��B1��4��2��C1��1��1����
����3��A1��2��4��B1��4��2��C1��1��1����
��������
��1���������⽨������ϵ���ɣ�
��2���ɵ�C������ϵ�е�λ�õó�C�����꣬���ݹ��ɶ��������ABC���ߵij��������ó����ܳ���
��3�����ݸ���������ϵ�е�λ�õó��������꼴�ɣ�
�⣺��1����ͼ��
��2����ABC��ͼ��ʾ����C����1��1����
��AB=![]() ��AC=
��AC=![]() ��BC=
��BC=![]() ��
��
��������ABC���ܳ���![]() ��
��
��3����A1B1C1��ͼ��ʾ��
A1��2��4��B1��4��2��C1��1��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
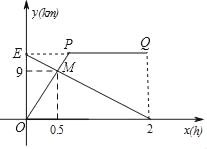
����Ŀ���������г���A�س���ǰ��B�أ�ͬʱ�Ҳ��д�B�س���ǰ��A�أ���ͼ������OPQ���߶�EF���ֱ��ʾ�ס���������A�صľ���y����y������������ʱ��x��h��֮��ĺ�����ϵ����OP��EF�ཻ�ڵ�M��
��1�����߶�OP��Ӧ��y����x�ĺ�����ϵʽ������ע���Ա���x��ȡֵ��Χ����
��2����y����x�ĺ�����ϵʽ�Լ�A��B����֮��ľ��룻
��3�����A��B��������ѡһ��������ѡ���� ���⣮
A��ֱ��д����������Сʱ���ס����������3km��
B����ס������˵ľ���Ϊs��km����ֱ��д��s��x�ĺ�����ϵʽ����ע��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ű�����,ǣ����ȫ���������,�����ij��ѧ�����˰��ľ��,ͼ�Ǹ��ݸ�У���꼶ij��ѧ��Ϊ�Ű��������������ƵIJ�����������ͳ��ͼ������ͳ��ͼ.

(1)��ð�ѧ��������;
(2)��ȫ����ͳ��ͼ;
(3)����У���꼶��800��,�ݴ�����,������Ƹ�У���꼶ѧ����������Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲO��ֱ��AB=10����һ������Ϊ6�Ķ���CD�ڻ�AB�ϻ�������C����D�ֱ����A����B�غϣ�����E��F��AB�ϣ�EC��CD��FD��CD�� 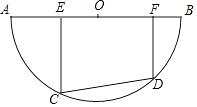
��1����֤��EO=OF��
��2������OC�������ECO����һ���ڽǵ���45�㣬���߶�EF�ij���
��3��������CD�ڻ�AB�ϻ���ʱ�������CE=x���ı���CDFE���ΪS���ܳ�Ϊl���ʣ�S��l�Ƿ�ֱ�����x�ı仯���仯��������ѧ�ĺ���֪ʶֱ��д�����ǵĺ�������ʽ��������������˵����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A,B,C��ͬһֱ����,�߶�AB=10cm��AC=6cm,M��AB���е�, N��AC���е�,���߶�MN�ij�����_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡij���ճ�Ϊȫ�˻������һ��ɱ�Ϊÿ��20Ԫ�Ĺ���Ʒ��Ͷ���г���������ÿ���������y���������ۼ�x��Ԫ/������һ�κ��������ۼ�Ϊ22Ԫ/��ʱ��ÿ��������Ϊ780�������ۼ�Ϊ25Ԫ/��ʱ��ÿ��������Ϊ750����
��1����y��x�ĺ�����ϵʽ��
��2������ù���Ʒ�ۼ���߲�����ÿ��30Ԫ����ô�ۼ۶�Ϊÿ������Ԫʱ�����ճ����۸ù���Ʒÿ���õ����������������Ƕ���Ԫ��������=�ۼ�-�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�����һ�����֣��ٻش��������⣮
��֪��ƽ��������P1��x1��y1����P2��x2��y2�����������ľ���P1P2=![]() ��ͬʱ�����������ڵ�ֱ�����������ƽ�����������ֱ��������ʱ���������빫ʽ�ɼ�Ϊ|x2��x1|��|y2��y1|��
��ͬʱ�����������ڵ�ֱ�����������ƽ�����������ֱ��������ʱ���������빫ʽ�ɼ�Ϊ|x2��x1|��|y2��y1|��
��1����֪A��3��3����B����2����1��������A��B�����ľ��룻
��2����֪A��B��ƽ����y���ֱ���ϣ���A��������Ϊ7����B��������Ϊ��2������A��B�����ľ��룻
��3����֪һ�������θ���������ΪA��0��5����B����3��2����C��3��2���������жϴ������ε���״��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P1��P2�Ƿ���������y= ![]() ��k��0���ڵ�һ����ͼ���ϵ����㣬��A1������Ϊ��4��0��������P1OA1���P2A1A2��Ϊ����ֱ�������Σ����е�P1��P2Ϊֱ�Ƕ��㣮
��k��0���ڵ�һ����ͼ���ϵ����㣬��A1������Ϊ��4��0��������P1OA1���P2A1A2��Ϊ����ֱ�������Σ����е�P1��P2Ϊֱ�Ƕ��㣮 
��1�����������Ľ���ʽ��
��2������P2�����꣮ �ڸ���ͼ��ֱ��д���ڵ�һ�����ڵ�x����ʲô����ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ��
�ĺ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C���㣩���� ![]() ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý�
ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý� ![]() CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA.�����½�������ȷ�ĸ����У� ��.
CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA.�����½�������ȷ�ĸ����У� ��.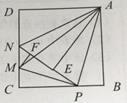
�� ![]() CMP��
CMP�� ![]() BPA��
BPA��
���ı���AMCB��������ֵΪ10��
�۵�PΪBC�е�ʱ��AEΪ�߶�NP���д��ߣ�
���߶�AM����СֵΪ2 ![]() ��
��
�ݵ� ![]() ABP��
ABP�� ![]() ANDʱ��BP=4
ANDʱ��BP=4 ![]() -4.
-4.
A.�٢ڢ�
B.�ڢۢ�
C.�٢ܢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com