
 如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.分析 (1)直接利用直角三角形中30°所对的边等于斜边的一半求出即可;
(2)根据题意可知,图中AB=50m,AD⊥BC,且BD=CD,∠AOD=30°,OA=80m;再利用垂径定理及勾股定理解答即可.
解答 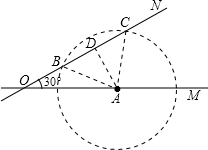 解:(1)过点A作AD⊥ON于点D,
解:(1)过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD=$\frac{1}{2}$BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD=$\frac{1}{2}$OA=$\frac{1}{2}$×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{5{0}^{2}-4{0}^{2}}$=30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即$\frac{18000}{60}$=300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒.
点评 此题考查的是垂径定理与勾股定理在实际生活中的运用,解答此题的关键是卡车在哪段路上运行时对学校产生影响.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
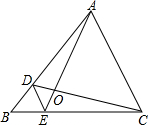 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )| A. | 有且只有1个 | |
| B. | 有且只有2个 | |
| C. | 组成∠E的角平分线 | |
| D. | 组成∠E的角平分线所在的直线(E点除外) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
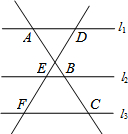 如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知$\frac{AB}{BC}=\frac{3}{2}$,则$\frac{DE}{DF}$的值为( )
如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知$\frac{AB}{BC}=\frac{3}{2}$,则$\frac{DE}{DF}$的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com