如图所示，在宽为16m，长为20m的矩形耕地上，修筑同样宽的两条道路（互相垂直），把耕地分成大小不等的四块试验田，要使试验田的面积为285m2，道路应为多宽？
科目：初中数学 来源：北京市2017-2018学年八年级下学期期中考试数学试卷 题型：解答题
已知：如图，在矩形ABCD中，AB=8，BC=4．在AD上取一点E，AE=1，点F是AB边上的一个动点，以EF为一边作菱形EFMN，使点N落在CD边上，点M落在矩形ABCD内或其边上．若AF=x，△BFM的面积为S．
（1）当四边形EFMN是正方形时，求x的值；
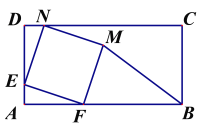
（2）当四边形EFMN是菱形时，求S与x的函数关系式；
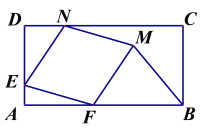
（3）当x= 时，△BFM的面积S最大；当x= 时，△BFM的面积S最小；
（4）在△BFM的面积S由最大变为最小的过程中，请直接写出点M运动的路线长： 。
查看答案和解析>>
科目：初中数学 来源：北京市2017-2018学年八年级下学期期中考试数学试卷 题型：填空题
阅读下面材料：
在数学课上，老师提出如下问题：
尺规作图：作对角线等于已知线段的菱形．
已知：两条线段a、b．
求作：菱形AMBN,使得其对角线分别等于b和2a．
尺规作图：作对角线等于已知线段的菱形．
已知：两条线段a、b．
求作：菱形AMBN,使得其对角线分别等于b和2a．
小军的作法如下：
如图
(1)画一条线段AB等于b；
(2)分别以A、B为圆心，大于
AB的长为半径，
在线段AB的上下各作两条弧，两弧相交于P、Q两点；
(3)作直线PQ交AB于O点；
(4)以O点为圆心，线段a的长为半径作两条弧，交直线PQ于M、N两点，连接AM、AN、BM、BN．所以四边形AMBN就是所求的菱形.
如图
(1)画一条线段AB等于b；
(2)分别以A、B为圆心，大于AB的长为半径，
在线段AB的上下各作两条弧，两弧相交于P、Q两点；
(3)作直线PQ交AB于O点；
(4)以O点为圆心，线段a的长为半径作两条弧，交直线PQ于M、N两点，连接AM、AN、BM、BN．所以四边形AMBN就是所求的菱形.
老师说：“小军的作法正确．”
该上面尺规作图作出菱形AMBN的依据是_______________________________
查看答案和解析>>
科目：初中数学 来源：北京市2017-2018学年八年级下学期期中考试数学试卷 题型：填空题
如图，在□ABCD中，AB=4，BC=7，∠ABC的平分线BE交AD于点E，则DE=____________.
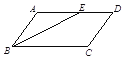
查看答案和解析>>
科目：初中数学 来源：青岛版数学八年级上学期第1-3章阶段性测评试卷 题型：解答题
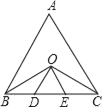
如图．在等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC．
（1）试判定△ODE的形状，并说明你的理由；
（2）线段BD、DE、EC三者有什么关系？写出你的判断过程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
有两个不相等的实数根，那么
的值，其中
，
，
，
，
．
，
，则
D. 