【题目】如图,已知点O为两内角平分线交点，∠A= 80°，则∠BOC=_______ 。

参考答案：

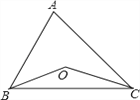
【答案】130度

【解析】（1）先根据三角形内角和定理求出∠ABC+∠ACB的度数，再根据BO、CO分别平分∠ABC与∠ACB求出∠1+∠2的度数，由三角形内角和定理即可得出∠BOC的度数；

解：如图所示，

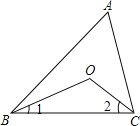
∵∠A=80°，
∴∠ABC+∠ACB=180°-80°=100°．
∵BO、CO分别是∠ABC、∠ACB的角平分线，
∴∠1+∠2=（∠ABC+∠ACB）=×100°=50°，
∴∠BOC=180°-（∠1+∠2）=180°-50°=130°．

“点睛”本题考查的是三角形内角和定理以及角平分线的性质，熟知三角形内角和是180°是解答此题的关键．求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件以及三角形的外角通常情况下是转化为内角来解决．

关闭