练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

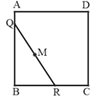
    【题目】如图，正方形ABCD的边长为4，将长为4的线段QR的 两 端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从点B出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为_____________.

    【答案】16－4π

    【解析】根据题意得点M到正方形各顶点的距离都为2，点M所走的运动轨迹为以正方形各顶点为圆心，以2为半径的四个扇形，

    ∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积。

    而正方形ABCD的面积为4×4=16,4个扇形的面积为=4π，

    ∴点M所经过的路线围成的图形的面积为164π.

    故答案为164π

    点睛: 根据直角三角形的性质，斜边上的中线等于斜边的一半，可知：点M到正方形各顶点的距离都为2，故点M所走的运动轨迹为以正方形各顶点为圆心，以2为半径的四个扇形，点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知两个有理数的和比其中任何一个加数都小 ，那么一定是 （ ）

    A. 这两个有理数同为正数 B. 这两个有理数同为负数

    C. 这两个有理数异号 D. 这两个有理数中有一个为零

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1．tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y=ax2+bx+c经过点A、B、C．

    （1）求抛物线的解析式；

    （2）若点P是第二象限内抛物线上的动点，其横坐标为t，

    ①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求出当△CEF与△COD相似时，点P的坐标；

    ②是否存在一点P，使△PCD得面积最大？若存在，求出△PCD的面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是( )

    A. 3x﹣x=3 B. x2x3=x5 C. （x2）3=x5 D. （2x）2=2x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解：m2﹣mn=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式中，从左到右的变形是因式分解的是（ ）
    A.（x+3y）（x﹣3y）=x2﹣9y2
    B.a（x+y+1）=ax+ay+a
    C.4x2﹣1=（2x+1）（2x﹣1）
    D.a2c﹣a2b+1=a2（c﹣b）+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据：8,1,4,3,x的平均数为x,则这组数据的众数是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

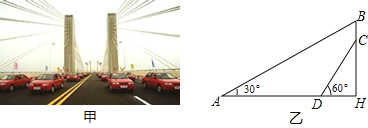
    【题目】某大桥采用低塔斜拉桥桥型（如甲图），图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索CD与水平桥面的夹角是60°，两拉索顶端的距离BC为2米，两拉索底端距离AD为20米，请求出立柱BH的长．（结果精确到0.1米， ≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一般地，n个相同的因数a相乘（即） a×a×a … a记 为an．如2×2×2＝23＝8，此时，3叫做以2为底8的对数，记为log28（即log28＝3）请探究log24、log216、log264之间的数量关系_______ 。

    查看答案和解析>>

    同步练习册答案