练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发生了求救信号，一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里/时的速度前往救援，求海警船到达事故船C处所需的大约时间．(参考数据：sin53°≈0.8，cos53°≈0.6)

    【答案】（小时）.

    【解析】试题分析：作CD⊥AB于点D，根据Rt△ACD的三角函数求出CD的长度，然后根据Rt△CBD的三角函数求出BC的长度，然后根据时间=路程÷速度得出答案.

    试题解析：作CD⊥AB于点D，在Rt△ACD中，AC=80，∠CAB=30°， ∴CD=40(海里)，

    在Rt△CBD中，CB=≈=50(海里)，∴航行的时间t==1.25(h)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，如图1，抛物线过点且对称轴为直线点Ｂ为直线OA下方的抛物线上一动点，点B的横坐标为m.

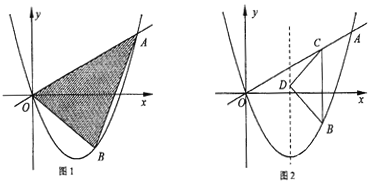
    （1）求该抛物线的解析式：

    （2）若△OAB的面积为S．求S关于m的函数关系式，并求出S的最大值．

    （3）如图2，过点B作直线BC∥y轴，交线段OA于点C，在抛物线的对称轴上是否存在点D，使△BCD是以D为直角顶点的等腰直角三角形？若存在，求出所有符合条件的点B的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx﹣1，若y随x的增大而增大，则它的图象经过（ ）
    A.第一、二、三象限
    B.第一、二、四象限
    C.第一、三、四象限
    D.第二、三、四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知AB=AC，∠BAC=90°，BC=6cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒2厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动，连接AD、AE，设运动时间为t秒．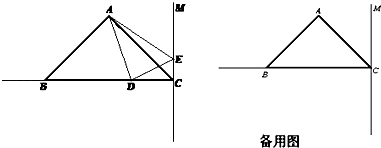
    （1）求AB的长；
    （2）当t为多少时，△ABD的面积为6cm2？
    （3）当t为多少时，△ABD≌△ACE，并简要说明理由．（可在备用图中画出具体图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】连续4个﹣3相乘可表示为（ ）

    A. 4×（﹣3） B. ﹣34 C. （﹣3）4 D. 4﹣3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一件产品原来每件的成本是1000元，由于连续两次降低成本，现在的成本是810元，则平均每次降低成本（　　）

    A. 8.5%B. 9%C. 9.5%D. 10%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若关于x的一元二次方程(m-2)x2-4x-2=0有两个实数根，则实数m的取值范围是（ ）

    A. m≥0B. m>0C. m≥0,m≠2D. m>0,m≠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a﹣b＝﹣4，c+d＝3，则（3b+c）﹣（3a﹣d）的值是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，直线CD与⊙O相切于C点，AC平分∠DAB．

    （1）求证：AD⊥CD；

    （2）若AD=2， ，求⊙O的半径R的长．

    查看答案和解析>>

    同步练习册答案