【题目】如图，已知△ABC 中，∠ABC＝45°，F 是高 AD 和 BE 的交点，∠CAD＝30°，CD＝4，则线段 BF 的长度为（ ）
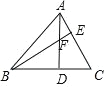
A. 6 B. 7 C. 8 D. 9
智能训练练测考系列答案科目：初中数学 来源： 题型：
【题目】如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m.
（结果精确到0.1m。参考数据：tan20°≈0.36,tan18°≈0.32）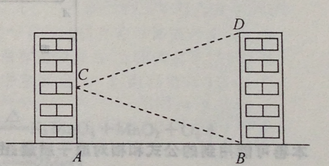
（1）求∠BCD的度数.
（2）求教学楼的高BD
查看答案和解析>>
科目：初中数学 来源： 题型：
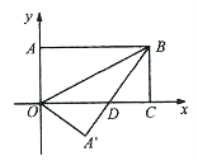
【题目】如图，把长方形纸片OABC放入平面直角坐标系中，使OC、OA分别与x轴，y轴重合，连接OB，将长方形纸片OABC沿OB折叠，使点A落在点A，的位置，A，B与x轴交于D，若点B的坐标为（4，2），则点A，的坐标为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
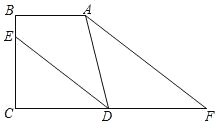
【题目】如图，AB⊥BC于点B，DC⊥BC于点C，DE平分∠ADC交BC于点E，点F为线段CD延长线上一点，∠BAF＝∠EDF．
(1)求证：∠DAF＝∠F；
(2)在不添加任何辅助线的情况下，请直接写出所有与∠CED互余的角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠E＝50°，∠BAC＝50°，∠D＝110°，求∠ABD的度数．
请完善解答过程，并在括号内填写相应的理论依据．
解：∵∠E＝50°，∠BAC＝50°，（已知）
∴∠E＝ （等量代换）
∴ ∥ ．（ ）
∴∠ABD+∠D＝180°．（ ）
∴∠D＝110°，（已知）
∴∠ABD＝70°．（等式的性质）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0），C（﹣1，0）．
（1）将△ABC向右平移5个单位，再向下平移4个单位得△A1B1C1，图中画出△A1B1C1，平移后点A的对应点A1的坐标是______．
（2）将△ABC沿x轴翻折△A2BC，图中画出△A2BC，翻折后点A对应点A2坐标是______．
（3）将△ABC向左平移2个单位，则△ABC扫过的面积为______．
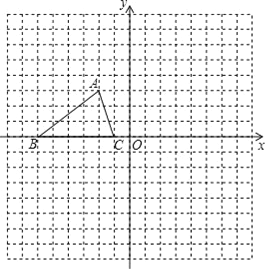
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．
小明的解题思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．
问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并完成填空．
你能比较 
和 
的大小吗?
为了解决这个问题，先把问题一般化，比较 
和 
（ 
，且 
为整数）的大小．然后从分析 
，
，
的简单情形入手，从中发现规律，经过归纳、猜想得出结论．
（1）通过计算（可用计算器）比较下列（1）-（7）组两数的大小：（在横线上填上 " 
"" 
“或”
"）
（1） 
；（2）
；（3）
；（4）
；（5）
；（6）
；（7）
；
（2）归纳第（1）问的结果，可以猜想出 
和 的大小关系；
（3）根据以上结论，可以得出 和 的大小关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图用点A(3，1)表示放置3个胡萝卜、1棵青菜，点B(2，3)表示放置2个胡萝卜、3棵青菜．
(1)请你写出其他各点C，D，E，F所表示的意义；
(2)若一只兔子从A到达B(顺着方格线走)，有以下几条路可以选择：①A→C→D→B；②A→F→D→B；③A→F→E→B，帮可爱的小白兔选一条路，使它吃到的食物最多．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
