
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

【答案】(1)![]() ;(2)(-6,0)(-2,0)
;(2)(-6,0)(-2,0)
【解析】分析:(1)利用反比例函数图象上点的坐标特征可求出点A、B的坐标,再利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标特征可求出点C的坐标,设点P的坐标为(x,0),根据三角形的面积公式结合S△ACP=![]() S△BOC,即可得出|x+4|=2,解之即可得出结论.
S△BOC,即可得出|x+4|=2,解之即可得出结论.
详解:(1)∵点A(m,3),B(﹣6,n)在双曲线y=![]() 上,
上,
∴m=2,n=﹣1,
∴A(2,3),B(﹣6,﹣1).
将(2,3),B(﹣6,﹣1)代入y=kx+b,
得:![]() ,解得
,解得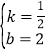 .
.
∴直线的解析式为y=![]() x+2.
x+2.
(2)当y=![]() x+2=0时,x=﹣4,
x+2=0时,x=﹣4,
∴点C(﹣4,0).
设点P的坐标为(x,0),
∵S△ACP=![]() S△BOC,A(2,3),B(﹣6,﹣1),
S△BOC,A(2,3),B(﹣6,﹣1),
∴![]() ×3|x﹣(﹣4)|=
×3|x﹣(﹣4)|=![]() ×
×![]() ×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
解得:x1=﹣6,x2=﹣2.
∴点P的坐标为(﹣6,0)或(﹣2,0).



科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:

(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数![]() ,
,![]() ,
,![]() 在数轴上的位置如下图所示:
在数轴上的位置如下图所示:
![]()
(1)若![]() ,求
,求![]() 的值.
的值.
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 对应的点分别为
对应的点分别为![]() ,
,![]() ,
,![]() ,问在数轴上是否存在一点
,问在数轴上是否存在一点![]() ,使
,使![]() 与
与![]() 的距离是
的距离是![]() 与
与![]() 的距离的3倍.若存在,请求出
的距离的3倍.若存在,请求出![]() 点对应的有理数;若不存在,请说明理由.
点对应的有理数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数,定义一种新运算“![]() ”,请仔细观察下列各式中的运算规律:1
”,请仔细观察下列各式中的运算规律:1![]() 2=
2=![]() =2,
=2,
![]() ,
,![]()
回答下列问题:
(1)计算:![]() =_____;
=_____;![]() =_____.
=_____.
(2)若a≠b,则![]() _____
_____![]() (填入“
(填入“![]() ”或“
”或“![]() ”
” ![]()
(3)若有理数a,b的取值范围在数轴上的对应点如图所示,且![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-8)+10-2+(-1); (2)12-7×(-4)+8÷(-2);
(3)(![]() )÷(-
)÷(-![]() ); (4)-14-(1+0.5)×
); (4)-14-(1+0.5)×![]() ÷(-4)2.
÷(-4)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在等腰△ABC中,AB=AC=![]() ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒![]() 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
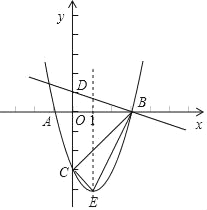
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com