Question

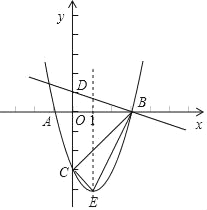
【题目】如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，直线y=﹣x+1与y轴交于点D．

（1）求抛物线的解析式；

（2）证明：△DBO∽△EBC；

（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线解析式为y=x2﹣2x﹣3；（2）见解析；（3）存在，P点坐标为（1，﹣1）或P（1， ）或（1，﹣）或（1，﹣3+）或（1，﹣3﹣）时，△PBC是等腰三角形．理由：见解析

【解析】试题分析：（1）设交点式y=a（x+1）（x-3），则-3a=-3，然后求出a得到抛物线解析式；

（2）先把抛物线解析式配成顶点式得到E（1，-4），再利用一次函数解析式确定D（0，1），则利用两点间的距离公式可计算出BC=3，BE=2，CE=，BD=，从而得到，然后根据相似三角形的判定方法可判断△BCE∽△BDO；

（3）设P（1，m），则利用两点间的距离公式可得BC2=18，PB2=m2+4，PC2=（m+3）2+1，然后讨论：当PB=PC时，△PBC是等腰三角形，则m2+4=（m+3）2+1；当PB=BC时，△PBC是等腰三角形，则m2+4=18；当PC=BC时，△PBC是等腰三角形，则（m+3）2+1=18，接着分别解关于m的方程求出m，从而得到满足条件的P点坐标．

试题解析：（1）解：抛物线的解析式为y=a（x+1）（x-3），

即y=ax2-2ax-3a，

∴-3a=-3，解得a=1，

∴抛物线解析式为y=x2-2x-3；

（2）证明：∵y=x2-2x-3=（x-1）2-4，

∴E（1，-4），

当x=0时，y=-x+1=1，则D（0，1），

∵B（3，0），A（-1，0），C（0，-3），

∴BC=，BE=，CE=，BD=，

∵， ， ，

∴，

∴△BCE∽△BDO；

（3）存在，

理由：抛物线的对称轴为直线x=1，设P（1，m），则BC2=18，PB2=（1-3）2+m2=m2+4，PC2=（m+3）2+1，

当PB=PC时，△PBC是等腰三角形，则m2+4=（m+3）2+1，解得m=-1，此时P（1，-1），

当PB=BC时，△PBC是等腰三角形，则m2+4=18，解得m=±，此时P（1， ）或（1，-）

当PC=BC时，△PBC是等腰三角形，则（m+3）2+1=18，解得m=-3±，此时P（1，-3+）或（-3-），

综上所述，P点坐标为（1，﹣1）或P（1， ）或（1，﹣）或（1，﹣3+）或（1，﹣3﹣）时，△PBC是等腰三角形．