
【题目】有理数![]() ,
,![]() ,
,![]() 在数轴上的位置如下图所示:
在数轴上的位置如下图所示:
![]()
(1)若![]() ,求
,求![]() 的值.
的值.
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 对应的点分别为
对应的点分别为![]() ,
,![]() ,
,![]() ,问在数轴上是否存在一点
,问在数轴上是否存在一点![]() ,使
,使![]() 与
与![]() 的距离是
的距离是![]() 与
与![]() 的距离的3倍.若存在,请求出
的距离的3倍.若存在,请求出![]() 点对应的有理数;若不存在,请说明理由.
点对应的有理数;若不存在,请说明理由.
【答案】(1)2014;(2)存在一点![]() ,使
,使![]() 与
与![]() 的距离是
的距离是![]() 与
与![]() 的距离的3倍.且
的距离的3倍.且 ![]() 点对应的有理数为0或2.
点对应的有理数为0或2.
【解析】
(1)首先根据数轴判断出绝对值里式子的正负性,然后凭借绝对值的意义去掉绝对值符号针对m进行化简即可,求出m的代数式后代入求值即可.
(2)设P点对应的数为x,然后分情况讨论:①当P点在A点的左边时;②当P点在A点与C点之间时;③当P点在C点右边时.
(1) 由数轴可得:![]() ,
,![]() ,
,![]() ,
,
∴![]()
= ![]()
=![]()
∴![]() =
=![]() =2014
=2014
(2)存在,设P点对应的数为x,
则当P点在A点左侧时:![]()
解得:![]() (不合题意,舍去),
(不合题意,舍去),
当P点在A点与C点之间时:![]() ,
,
解得:![]() ,
,
当P点在C点右侧时:![]() ,
,
解得:![]() ,
,
综上所述,存在一点![]() ,使
,使![]() 与
与![]() 的距离是
的距离是![]() 与
与![]() 的距离的3倍.且
的距离的3倍.且 ![]() 点对应的有理数为0或2.
点对应的有理数为0或2.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生在2019年10月第2周星期五股市收盘时,以每股9元的价格买进某公司的股票1000股,在11月第2周的星期一至星期五,该股票每天收盘时每股的涨跌(单位:元)情况如下表:
时 间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
每股涨跌/元 | 0 | -0.32 | +0.47 | -0.21 | +0.56 |
注:表中记录的数据为每天收盘价格与前一天收盘价格的变化量,星期一的数据是与上星期五收盘价格的变化量.
(1)请你判断在11月的第2周内,该股票价格收盘时,价格最高的是哪一天?
(2)在11月第2周内,求李先生购买的股票每股每天平均的收盘价格.(结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
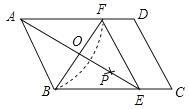
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①、②、③行第n个数分别为 ; ; .
(2)取每行数的第九个数,计算这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.

(2)如图2,若C为线段AB上任意一点,满足AC+CB=acm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上的一点,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com