练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】观察下面三行数：

    ﹣2，4，﹣8，16，﹣32，64 …①

    0，6，﹣6，18，﹣30，66…②

    ﹣1，2，﹣4，8，﹣16，32…③

    （1）第①、②、③行第n个数分别为　 　；　 　；　 　．

    （2）取每行数的第九个数，计算这三个数的和．

    【答案】（1）（﹣2）n；（﹣2）n+2；（﹣2）n；（2）﹣1278

    【解析】

    （1）第一行的第n个数用（﹣2）n表示，第二行的第n个数用（﹣2）n+2表示，第三行的第n个数用（﹣2）n表示；

    （2）根据（1）中的规律求得每行数的第九个数，计算这三个数的和即可．

    解：（1）∵第1行中，第1个数＝（﹣2）1＝﹣2，第2个数＝（﹣2）2＝4，第3个数＝（﹣2）3＝﹣8，…，故第n个数＝（﹣2）n．

    第2行数等于第1行相应的数加2；

    第3行数等于第1行相应的数的一半；

    故答案为：（﹣2）n；（﹣2）n+2；（﹣2）n；

    （2）当n＝9时，（﹣2）9＝﹣512；（﹣2）9+2＝﹣510；×（﹣2）9＝﹣256；

    ∴这三个数的和＝﹣1278．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

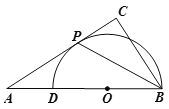
    【题目】如图，在△ABC中，∠ACB=90°，点D是AB上一点，以BD为直径的⊙O和AC相切于点P．

    （1）求证：BP平分∠ABC；

    （2）若PC=1，AP=3，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为、、，求△ABC的面积．

    小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法．

    请回答：

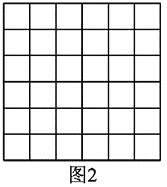
    （1）①图1中△ABC的面积为________；

    ②图1中过O点画一条线段MN，使MN＝2AB，且M、N在格点上．

    （2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．利用构图法在图2中画出三边长分别为、2、的格点△DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，半径为1的小圆与半径为2的大圆，有一个公共点与数轴上的原点重合，两圆在数轴上做无滑动的滚动，小圆的运动速度为每秒π个单位，大圆的运动速度为每秒2π个单位，（1）若小圆不动，大圆沿数轴来回滚动，规定大圆向右滚动的时间记为正数，向左滚动时间即为负数，依次滚动的情况录如下（单位：秒）：﹣1，+2，﹣4，﹣2，+3，+6

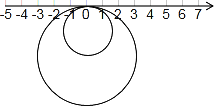
    （1）第　 　 次滚动后，大圆与数轴的公共点到原点的距离最远；

    （2）当大圆结束运动时，大圆运动的路程共有多少？此时两圆与数轴重合的点之间的距离是多少？（结果保留π）

    （3）若两圆同时在数轴上各自沿着某一方向连续滚动，滚动一段时间后两圆与数轴重合的点之间相距9π，求此时两圆与数轴重合的点所表示的数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一楼房AB后有一假山，山坡斜面CD与水平面夹角为30°，坡面上点E处有一亭子，测得假山坡脚C与楼房水平距离BC=10米，与亭子距离CE=20米，小丽从楼房顶测得点E的俯角为45°．求楼房AB的高（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有理数，，在数轴上的位置如下图所示：

    （1）若，求的值.

    （2）若，，，且，，对应的点分别为，，，问在数轴上是否存在一点，使与的距离是与的距离的3倍.若存在，请求出点对应的有理数；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，E为正方形ABCD的边BC上一点，F为边BA延长线上一点，且CE＝AF．

    （1）求证：DE⊥DF；

    （2）如图2，若点G为边AB上一点，且∠BGE＝2∠BFE，△BGE的周长为16，求四边形DEBF的面积；

    （3）如图3，在（2）的条件下，DG与EF交于点H，连接CH且CH＝5，求AG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于有理数，定义一种新运算“”，请仔细观察下列各式中的运算规律：12==2，

    ，

    回答下列问题：

    (1)计算：=_____；=_____.

    (2)若a≠b，则_____(填入“”或“”

    (3)若有理数a，b的取值范围在数轴上的对应点如图所示，且，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下列一段文字，再解答问题
    已知在平面内有两点，，其两点间的距离公式为，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为或
    已知点，，试求A，B两点间的距离；
    已知点A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为，试求A，B两点间的距离；
    已知点，，判断线段AB，BC，AC中哪两条是相等的？并说明理由．

    查看答案和解析>>

    同步练习册答案