
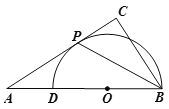
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OP,首先证明OP∥BC,推出∠OPB=∠PBC,由OP=OB,推出∠OPB=∠OBP,由此推出∠PBC=∠OBP;
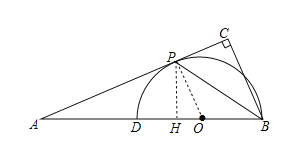
(2)作PH⊥AB于H.首先证明PC=PH=1,在Rt△APH中,求出AH,由△APH∽△ABC,求出AB、BH,由Rt△PBC≌Rt△PBH,推出BC=BH即可解决问题.
试题解析:
(1)连接OP,
∵AC是⊙O的切线,
∴OP⊥AC,
∴∠APO=∠ACB=90°,
∴OP∥BC,
∴∠OPB=∠PBC,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠PBC=∠OBP,
∴BP平分∠ABC;
(2)作PH⊥AB于H.则∠AHP=∠BHP=∠ACB=90°,
又∵∠PBC=∠OBP,PB=PB,
∴△PBC≌△PBH ,
∴PC=PH=1,BC=BH,
在Rt△APH中,AH=![]() ,
,
在Rt△ACB中,AC2+BC2=AB2
∴(AP+PC)2+BC2=(AH+HB)2,
即42+BC2=(![]() +BC)2,
+BC)2,
解得![]() .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中,对角线 BD 的垂直平分线 MN 与 AD 相交于点 M ,与 BD 相交于点 N ,连接 BM 、 DN .
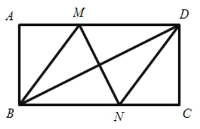
(1)求证: BN DM ;
(2)若 AB 4 , AD 8,求 MD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
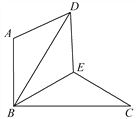
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,若函数y=![]() (x>0)的图象△ABC的边有公共点,则k的取值范围是( )
(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
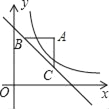
A. 5≤k≤20 B. 8≤k≤20 C. 5≤k≤8 D. 9≤k≤20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价180元,T恤每件定价60元,厂家在开展促销活动期间,向顾客提供了两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款;现在某客户要到该厂购买夹克30件,T恤![]() 件(
件(![]() >
>![]() ).
).
(1)若该客户按方案①购买付款 元(用含![]() 的式子表示);若该客户按方案②购买付款 元(用含
的式子表示);若该客户按方案②购买付款 元(用含![]() 的式子表示).
的式子表示).
(2)当![]() 时,通过计算说明方案①、方案②哪种方案购买较为合算?
时,通过计算说明方案①、方案②哪种方案购买较为合算?
(3)当![]() 时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某汽车行驶的路程![]()
![]() 与时间
与时间![]() (分钟)的函数关系图.
(分钟)的函数关系图.
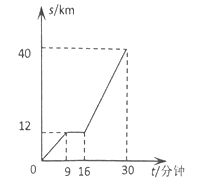
观察图中所提供的信息,解答下列问题:
(1)汽车在前![]() 分钟内的平均速度是 .
分钟内的平均速度是 .
(2)汽车在中途停了多长时间?
(3)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式
的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①、②、③行第n个数分别为 ; ; .
(2)取每行数的第九个数,计算这三个数的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com