
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
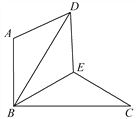
【答案】证明见解析.
【解析】试题分析:(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵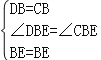 ,
,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:定义一种新运算“⊙”:
1⊙3=1×4+3=7,3⊙﹣1=3×4﹣1=11,5⊙4=5×4+4=24
4⊙(﹣3)=4×4﹣3=13,(﹣2)⊙(﹣5)=(﹣2)×4﹣5=﹣13,……
(1)写出一般结论:a⊙b=_____;
(2)如果a≠b,那么a⊙b_____b⊙a(填“=”或“≠”)
(3)先化简,再求值:(a﹣b)⊙(2a+3b).其中a=﹣![]() ,b=2019.
,b=2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
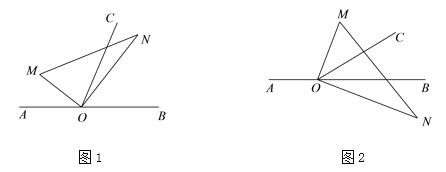
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=a,直接写出∠CON的度数(用含a的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在射线OB上方,另一边ON在直线AB的下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( ) 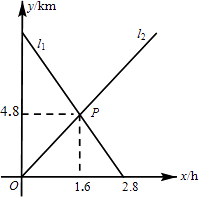
A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查学生的身体素质,随机抽取了某市的若干所初中学校,根据学校学生的肺活量指标等级绘制了相应的统计图,如图. 根据以上统计图,解答下列问题: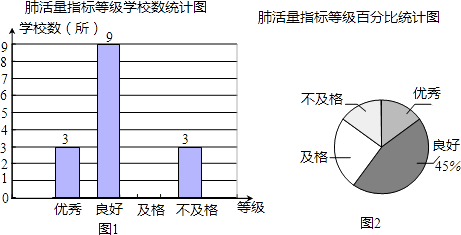
(1)这次调查共抽取了几所学校?请补全图1;
(2)估计该市140所初中学校中,有几所学校的肺活量指标等级为优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A. 6 B. 4![]() C. 3
C. 3![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月19日为中国旅游日,衢州推出“读万卷书,行万里路,游衢州景”的主题系列旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点;下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山这两个地的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.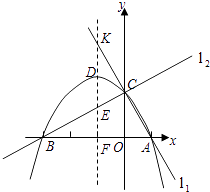
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com