
【题目】如图,在□ABCD中,E、F为对角线BD上的两点,且∠DAE=∠BCF.
(1)求证:AE=CF;
(2)求证:AE∥CF.

【答案】(1)证明见解析(2)证明见解析
【解析】
试题(1)根据平行四边形性质得出AB=DC,AD=BC,AB∥CD,AD∥BC,推出∠ABF=∠CDE,∠ADE=∠CBF,根据全等三角形的判定推出△DAE≌△BCF,即可得;
(2)由△DAE≌△BCF,得出∠DEA=∠BFC,从而得∠AEF=∠DFC,继而得AE∥CF.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC,AB∥CD,AD∥BC,
∴∠ABF=∠CDE,∠ADE=∠CBF,
在△DAE和△BCF中,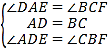 ,
,
∴△DAE≌△BCF(ASA),∴AE=CF;
(2)∵△DAE≌△BCF,∴∠DEA=∠BFC,∴∠AEF=∠DFC,∴AE∥CF.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
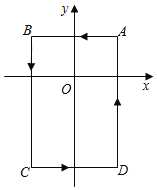
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
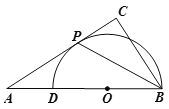
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
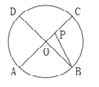
【题目】如图,A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿OC→![]() →DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为
→DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为![]() (s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
(s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
A. 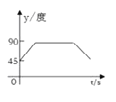 B.
B. 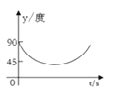 C.
C. 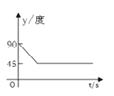 D.
D. 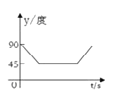
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:

(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:

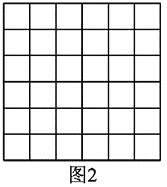
(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF.
的格点△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的小圆与半径为2的大圆,有一个公共点与数轴上的原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位,(1)若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动的时间记为正数,向左滚动时间即为负数,依次滚动的情况录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,+6
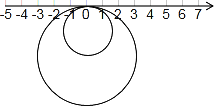
(1)第 次滚动后,大圆与数轴的公共点到原点的距离最远;
(2)当大圆结束运动时,大圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是多少?(结果保留π)
(3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距9π,求此时两圆与数轴重合的点所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数,定义一种新运算“![]() ”,请仔细观察下列各式中的运算规律:1
”,请仔细观察下列各式中的运算规律:1![]() 2=
2=![]() =2,
=2,
![]() ,
,![]()
回答下列问题:
(1)计算:![]() =_____;
=_____;![]() =_____.
=_____.
(2)若a≠b,则![]() _____
_____![]() (填入“
(填入“![]() ”或“
”或“![]() ”
” ![]()
(3)若有理数a,b的取值范围在数轴上的对应点如图所示,且![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com