
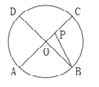
【题目】如图,A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿OC→![]() →DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为
→DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为![]() (s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
(s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
A. 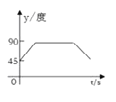 B.
B. 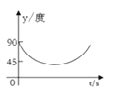 C.
C. 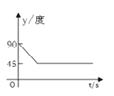 D.
D. 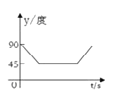
科目:初中数学 来源: 题型:
【题目】已知数轴上A,B两点对应的数分别为-2和8,P为数轴上一点,对应的数为x.
(1)线段PA的长度可表示为_________(用含![]() 的式子表示);
的式子表示);
(2)在数轴上是否存在点P,使得PA-PB=6?若存在,求出x的值;若不存在,请说明理由;
(3)当P为线段AB的中点时,点A,B,P同时开始在数轴上分别以每秒3个单位长度,每秒2个单位长度,每秒1个单位长度沿数轴正方向运动,试问经过几秒,PB=2PA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价180元,T恤每件定价60元,厂家在开展促销活动期间,向顾客提供了两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款;现在某客户要到该厂购买夹克30件,T恤![]() 件(
件(![]() >
>![]() ).
).
(1)若该客户按方案①购买付款 元(用含![]() 的式子表示);若该客户按方案②购买付款 元(用含
的式子表示);若该客户按方案②购买付款 元(用含![]() 的式子表示).
的式子表示).
(2)当![]() 时,通过计算说明方案①、方案②哪种方案购买较为合算?
时,通过计算说明方案①、方案②哪种方案购买较为合算?
(3)当![]() 时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某汽车行驶的路程![]()
![]() 与时间
与时间![]() (分钟)的函数关系图.
(分钟)的函数关系图.
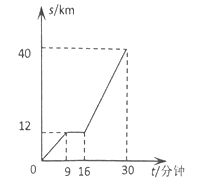
观察图中所提供的信息,解答下列问题:
(1)汽车在前![]() 分钟内的平均速度是 .
分钟内的平均速度是 .
(2)汽车在中途停了多长时间?
(3)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式
的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为建设美丽农村,村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为a的大正方形花坛和四个边长为b的小正方形花坛(阴影部分),空白区域铺设草坪,记S1表示地块甲中空白处铺设草坪的面积,S2表示地块乙中空白处铺设草坪的面积.
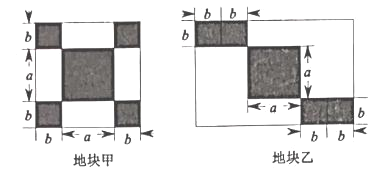
(1)S1=________,S2=________(用含a,b的代数式表示并化简) .
(2)若a=2b,求的![]() 值
值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于( )
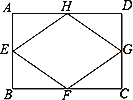
A. 20B. 10C. 4![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com