
ЁОЬтФПЁПЖЈвхЃКЖдгкИјЖЈЕФЖўДЮКЏЪ§y=aЃЈxЉhЃЉ2+kЃЈaЁй0ЃЉЃЌЦфАщЩњвЛДЮКЏЪ§ЮЊy=aЃЈxЉhЃЉ+kЃЌР§ШчЃКЖўДЮКЏЪ§y=2ЃЈx+1ЃЉ2Љ3ЕФАщЩњвЛДЮКЏЪ§ЮЊy=2ЃЈx+1ЃЉЉ3ЃЌМДy=2xЉ1ЃЎ
ЃЈ1ЃЉвбжЊЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЃЌдђЦфАщЩњвЛДЮКЏЪ§ЕФБэДяЪНЮЊ_____ЃЛ
ЃЈ2ЃЉЪдЫЕУїЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЕФЖЅЕудкЦфАщЩњвЛДЮКЏЪ§ЕФЭМЯѓЩЯЃЛ
ЃЈ3ЃЉШчЭМЃЌЖўДЮКЏЪ§y=mЃЈxЉ1ЃЉ2Љ4mЃЈmЁй0ЃЉЕФАщЩњвЛДЮКЏЪ§ЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкЕуBЁЂAЃЌЧвСНКЏЪ§ЭМЯѓЕФНЛЕуЕФКсзјБъЗжБ№ЮЊ1КЭ2ЃЌдкЁЯAOBФкВПЕФЖўДЮКЏЪ§y=mЃЈxЉ1ЃЉ2Љ4mЕФЭМЯѓЩЯгавЛЖЏЕуPЃЌЙ§ЕуPзїxжсЕФЦНааЯпгыЦфАщЩњвЛДЮКЏЪ§ЕФЭМЯѓНЛгкЕуQЃЌЩшЕуPЕФКсзјБъЮЊnЃЌжБНгаДГіЯпЖЮPQЕФГЄЮЊ![]() ЪБnЕФжЕЃЎ
ЪБnЕФжЕЃЎ

ЁОД№АИЁПy=xЉ5
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЖЈвхЃЌжБНгБфаЮЕУЕНАщЩњвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓГіЖЅЕуЃЌДњШыАщЩњКЏЪ§НтЮіЪНМДПЩЧѓНтЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЕНАщЩњКЏЪ§НтЮіЪНЃЌИљОнPЕуЕФзјБъЃЌзјБъБэЪОГізнзјБъЃЌШЛКѓЭЈЙ§PQгыxжсЕФЦНааЙиЯЕЃЌЧѓЕУQЕуЕФзјБъЃЌгЩPQЕФГЄСаЗНГЬЧѓНтМДПЩ.
ЯъНтЃКЃЈ1ЃЉЁпЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЃЌ
ЁрЦфАщЩњвЛДЮКЏЪ§ЕФБэДяЪНЮЊy=ЃЈxЉ1ЃЉЉ4=xЉ5ЃЌ
ЙЪД№АИЮЊy=xЉ5ЃЛ
ЃЈ2ЃЉЁпЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЃЌ
ЁрЖЅЕузјБъЮЊЃЈ1ЃЌЉ4ЃЉЃЌ
ЁпЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЃЌ
ЁрЦфАщЩњвЛДЮКЏЪ§ЕФБэДяЪНЮЊy=xЉ5ЃЌ
ЁрЕБx=1ЪБЃЌy=1Љ5=Љ4ЃЌ
ЁрЃЈ1ЃЌЉ4ЃЉдкжБЯпy=xЉ5ЩЯЃЌ
МДЃКЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЕФЖЅЕудкЦфАщЩњвЛДЮКЏЪ§ЕФЭМЯѓЩЯЃЛ
ЃЈ3ЃЉЁпЖўДЮКЏЪ§y=mЃЈxЉ1ЃЉ2Љ4mЃЌ
ЁрЦфАщЩњвЛДЮКЏЪ§ЮЊy=mЃЈxЉ1ЃЉЉ4m=mxЉ5mЃЌ
ЁпPЕуЕФКсзјБъЮЊnЃЌЃЈnЃО2ЃЉЃЌ
ЁрPЕФзнзјБъЮЊmЃЈnЉ1ЃЉ2Љ4mЃЌ
МДЃКPЃЈnЃЌmЃЈnЉ1ЃЉ2Љ4mЃЉЃЌ
ЁпPQЁЮxжсЃЌ
ЁрQЃЈЃЈnЉ1ЃЉ2+1ЃЌmЃЈnЉ1ЃЉ2Љ4mЃЉЃЌ
ЁрPQ=ЃЈnЉ1ЃЉ2+1ЉnЃЌ
ЁпЯпЖЮPQЕФГЄЮЊ![]() ЃЌ
ЃЌ
ЁрЃЈnЉ1ЃЉ2+1Љn=![]() ЃЌ
ЃЌ
Ёрn=![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжиЧьФГжабЇзщжЏЦпЁЂАЫЁЂОХФъМЖбЇЩњВЮМгЁАжБЯН20ФъЃЌЕудоаТжиЧьЁБзїЮФБШШќЃЌИУаЃНЋЪеЕНЕФВЮШќзїЮФНјааЗжФъМЖЭГМЦЃЌЛцжЦСЫШчЭМ1КЭШчЭМ2СНЗљВЛЭъећЕФЭГМЦЭМЃЌИљОнЭМжаЬсЙЉЕФаХЯЂЭъГЩвдЯТЮЪЬтЃЎ
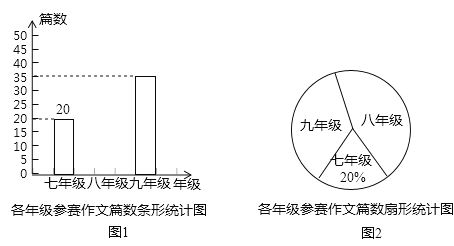
ЃЈ1ЃЉЩШаЮЭГМЦЭМжаОХФъМЖВЮШќзїЮФЦЊЪ§ЖдгІЕФдВаФНЧЪЧ ЖШЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉОЙ§ЦРЩѓЃЌШЋаЃга4ЦЊзїЮФШйЛёЬиЕШНБЃЌЦфжагавЛЦЊРДздЦпФъМЖЃЌбЇаЃзМБИДгЬиЕШНБзїЮФжаШЮбЁСНЦЊПЏЕЧдкаЃПЏЩЯЃЌЧыРћгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіЦпФъМЖЬиЕШНБзїЮФБЛбЁЕЧдкаЃПЏЩЯЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ЬнаЮABCDжа,ABЁЮCDЃЌЧвAB=2CDЃЌE. FЗжБ№ЪЧABЁЂBCЕФжаЕуЃЌEFгыBDЯрНЛгкЕуM.

(1)ЧѓжЄЃКЫФБпаЮCBEDЪЧЦНааЫФБпаЮ.
(2)ШєDB=9ЃЌЧѓBMЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЁЯІСКЭЁЯІТЛЅВЙЃЌЧвЁЯІСЃОЁЯІТЃЌдђЯТСаБэЪОЁЯІТЕФгрНЧЕФЪНзгжаЃКЂй90ЁуЉЁЯІТЃЛЂкЁЯІСЉ90ЁуЂл![]() ЃЈЁЯІС+ЁЯІТЃЉЃЛЂм
ЃЈЁЯІС+ЁЯІТЃЉЃЛЂм![]() ЃЈЁЯІСЉЁЯІТЃЉЃЎе§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЈЁЯІСЉЁЯІТЃЉЃЎе§ШЗЕФгаЃЈЁЁЁЁЃЉ
A. 4Иі B. 3Иі C. 2Иі D. 1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуAЃЌCЗжБ№дкxжсЃЌyжсЕФе§АыжсЩЯЃЌЧвOA=4ЃЌOC=3ЃЌШєХзЮяЯпОЙ§OЃЌAСНЕуЃЌЧвЖЅЕудкBCБпЩЯЃЌЖдГЦжсНЛACгкЕуDЃЌЖЏЕуPдкХзЮяЯпЖдГЦжсЩЯЃЌЖЏЕуQдкХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБPO+PCЕФжЕзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдквдAЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіPЃЌQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂBЁЂCЁЂDЮЊдВOЕФЫФЕШЗжЕуЃЌЖЏЕуPДгдВаФOГіЗЂЃЌбиOCЁњ![]() ЁњDOЕФТЗЯпзідШЫйдЫЖЏЃЌЕБЕуPдЫЖЏЕНдВаФOЪБСЂМДЭЃжЙ.ЩшдЫЖЏЪБМфЮЊ
ЁњDOЕФТЗЯпзідШЫйдЫЖЏЃЌЕБЕуPдЫЖЏЕНдВаФOЪБСЂМДЭЃжЙ.ЩшдЫЖЏЪБМфЮЊ![]() ЃЈsЃЉЃЌЁЯAPBЕФЖШЪ§ЮЊyЖШЃЌдђЯТСаЭМЯѓжаБэЪОy(ЖШ)гы t(s)жЎМфЕФКЏЪ§ЙиЯЕзюЧЁЕБЕФЪЧ ( )
ЃЈsЃЉЃЌЁЯAPBЕФЖШЪ§ЮЊyЖШЃЌдђЯТСаЭМЯѓжаБэЪОy(ЖШ)гы t(s)жЎМфЕФКЏЪ§ЙиЯЕзюЧЁЕБЕФЪЧ ( )
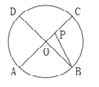
A. 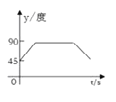 B.
B. 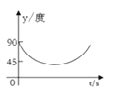 C.
C. 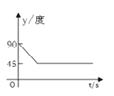 D.
D. 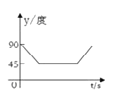
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКдкЪ§жсЩЯAЕуБэЪОЪ§aЃЌBЕуЪОЪ§bЃЌCЕуБэЪОЪ§cЃЌbЪЧзюаЁЕФе§ећЪ§ЃЌЧвaЃЌbТњзу![]() +(cЃ7)2=0ЃЎ
+(cЃ7)2=0ЃЎ
(1) a= ЃЌb= ЃЌc= ЃЎ
(2) ШєНЋЪ§жселЕўЃЌЪЙЕУAЕугыCЕужиКЯЃЌдђЕуBгыЪ§ БэЪОЕФЕужиКЯЃЎ
(3) ЕуAЃЌBЃЌCПЊЪМдкЪ§жсЩЯдЫЖЏЃЌШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ4ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌМйЩшtУыжгЙ§КѓЃЌШєЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЌЕуAгыЕуCжЎМфЕФОрРыБэЪОЮЊACЃЌЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЎдђAB= ЃЌAC= ЃЌBC= ЃЎ(гУКЌtЕФДњЪ§ЪНБэЪО)
(4) ЧыЮЪЃК3BCЃ2ABЕФжЕЪЧЗёЫцзХЪБМфtЕФБфЛЏЖјИФБф? ШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЙсГЙТфЪЕЪаЮЏеўИЎЬсГіЕФЁАОЋзМЗіЦЖЁБОЋЩёЃЌФГаЃЬижЦЖЈСЫвЛЯЕСаАяЗіAЁЂBСНЦЖРЇДхЕФМЦЛЎЃЌЯжОіЖЈДгФГЕидЫЫЭ152ЯфгуУчЕНAЁЂBСНДхбјжГЃЌШєгУДѓаЁЛѕГЕЙВ15СОЃЌдђЧЁКУФмвЛДЮаддЫЭъетХњгуУчЃЌвбжЊетСНжжДѓаЁЛѕГЕЕФдиЛѕФмСІЗжБ№ЮЊ12Яф/СОКЭ8Яф/СОЃЌЦфдЫЭљAЁЂBСНДхЕФдЫЗбШчБэЃК
ГЕаЭ | ФПЕФЕи | |
AДхЃЈдЊ/СОЃЉ | BДхЃЈдЊ/СОЃЉ | |
ДѓЛѕГЕ | ||
800 | 900 | |
аЁЛѕГЕ | 400 | 600 |
ЃЈ1ЃЉЧѓет15СОГЕжаДѓаЁЛѕГЕИїЖрЩйСОЃП
ЃЈ2ЃЉЯжАВХХЦфжа10СОЛѕГЕЧАЭљAДхЃЌЦфгрЛѕГЕЧАЭљBДхЃЌЩшЧАЭљAДхЕФДѓЛѕГЕЮЊxСОЃЌЧАЭљAЁЂBСНДхзмЗбгУЮЊyдЊЃЌЪдЧѓГіyгыxЕФКЏЪ§НтЮіЪНЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєдЫЭљAДхЕФгуУчВЛЩйгк100ЯфЃЌЧыФуаДГіЪЙзмЗбгУзюЩйЕФЛѕГЕЕїХфЗНАИЃЌВЂЧѓГізюЩйЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЮЊБп
ЮЊБп![]() ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌЩш
ЃЌЩш![]() НЛ
НЛ![]() ЕФЭтНЧЦНЗжЯп
ЕФЭтНЧЦНЗжЯп![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп![]() гк
гк![]() .
.
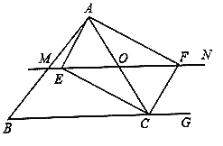
(1)ЧѓжЄЃК![]() ЃЛ
ЃЛ
(2)ЕБЕу![]() дЫЖЏЕНКЮДІЪБЃЌЫФБпаЮ
дЫЖЏЕНКЮДІЪБЃЌЫФБпаЮ![]() ЪЧОиаЮЃПВЂжЄУїФуЕФНсТлЃЛ
ЪЧОиаЮЃПВЂжЄУїФуЕФНсТлЃЛ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com