
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为 ![]() (即tan∠PAB=
(即tan∠PAB= ![]() ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.

(1)DE与BC是否平行,请说明理由;
(2)D、E、F分别为AB、AC、DC中点,连接BF,若![]() 四边形 ADEF=
四边形 ADEF=![]() 求
求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:数学兴趣小组在活动时,老师提出了这样一个问题:如图①,在Rt△ABC中,∠BAC=90°,BC=10,AD是BC边上的中线,求AD的长度.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,则AD=![]() AE
AE

在△ADC和△EDB中

∴△ADC≌△EDB
∴∠DBE=∠DCA,BE=AC
∴BE∥AC
∴∠EBA+∠BAC=180°
∵∠BAC=90°
∴∠EBA=90°
在△EBA和△CAB中

∴△EBA≌△CAB
∴AE=BC
∵BC=10
∴AD=![]() AE=
AE=![]() BC=5
BC=5
(1)若将上述问题中条件“BC=10”换成“BC=a”,其他条件不变,则可得AD= .
从上得到结论:直角三角形斜边上的中线,等于斜边的一半.
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形进而求解.
问题解决:(2)如图②,在四边形ABCD中,AD∥BC,∠D=90°,M是AB的中点.若CM=6.5,BC+CD+DA=17,求四边形ABCD的面积.
问题拓展:(3)如图③,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,∠DFE与∠AEF的度数满足数量关系:∠DFE=k∠AEF,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家住房户型呈长方形,平面图如下(单位:米).现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)

(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米.装修公司有A,B两种活动方案,如表:
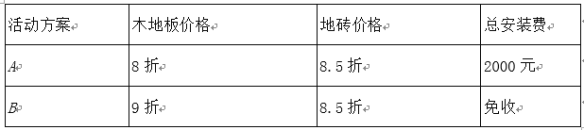
已知卧室2的面积为21平方米,则小方家应选择哪种活动,使铺设地面总费用(含材料费及安装费)更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠P=100°,则∠ACB的大小为__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com