
【题目】如图,将矩形纸片的两只直角分别沿EF、DF翻折,点B恰好落在AD边上的点B′处,点C恰好落在边B′F上.若AE=3,BE=5,则FC= . 
【答案】4
【解析】解:由题意得:B′E=BE=5,BF=B′F,∠BFE═∠EFB′,∠C′FD=∠DFC,
∴∠EFD=90°,
∴∠3+∠2=90°,
连接BB′,
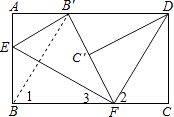
∴EF⊥BB′,
∴∠1+∠3=90°,
∴∠1=∠2,
∵AE=3,四边形ABCD是矩形,
∴∠A=∠C=90°,AD∥BC,
∴∠AB′B=∠1,AB′= ![]() =4,
=4,
∴∠AB′B=∠2,
∵CD=AB=8,
在△ABB′与△CDF中,
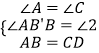 ,
,
∴△ABB′≌△CDF(AAS),
∴CF=AB′=4.
【考点精析】关于本题考查的勾股定理的概念和矩形的判定方法,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“ 1□3□9□7” 中的每个□内,填入![]() ,
,![]() ,
,![]() ,
,![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若1![]() 3×9□7= -4,请推算□内的符号;
3×9□7= -4,请推算□内的符号;
(3)在“1□3□9-7”的□内填入符号后,使计算所得数最小,直接写出这个最小数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A'B'C',图中标出了点B的对应点B'.利用网格点和三角板画图:
(1)补全△A'B'C'根据下列条件;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
(4)线段A'B'与AB的关系是 .△A'B'C'的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数y= ![]() (k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 , 写出符合题意的其中一条抛物线解析式 , 并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
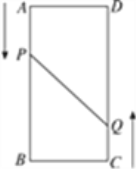
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com