
����Ŀ����֪��A��B�ֱ���x�ᡢy���ϵĶ��㣬��C��D��ij������ͼ���ϵĵ㣬���ı���ABCD��A��B��C��D�����������У�Ϊ������ʱ�������������Ϊ�˺���ͼ��İ��������Σ����磺��ͼ��������ABCD��һ�κ���y=x+1ͼ�������һ�����������Σ�
��1����ij������һ�κ���y=x+1��������ͼ������а��������εı߳���
��2����ij�����Ƿ���������y= ![]() ��k��0��������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
��k��0��������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
��3����ij�����Ƕ��κ���y=ax2+c��a��0��������ͼ��İ���������ΪABCD��C��D�е�һ��������Ϊ��3��4����д���������������������ϵ���һ���������� �� д���������������һ�������߽���ʽ �� ���ж���д���������ߵİ��������εĸ�������������ż�� ��
���𰸡�
��1���⣺��ͼ1��
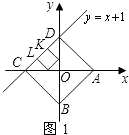
����A��x�������ᣬ��B��y�Ḻ������ʱ��
��OC=0D=1��
��������ABCD�ı߳�CD= ![]() ����OCD=��ODC=45�㣬
����OCD=��ODC=45�㣬
����A��x�Ḻ���ᡢ��B��y����������ʱ��
��С�����εı߳�Ϊa��
��CL=С�����εı߳�=DK=LK����3a=CD= ![]() ��
��
���a= ![]() ������С�����α߳�Ϊ
������С�����α߳�Ϊ ![]() ��
��
��һ�κ���y=x+1ͼ��İ��������εı߳�Ϊ ![]() ��
�� ![]()
��2���⣺��ͼ2����DE��CF�ֱ�ֱ��x��y�ᣬ

��֪��ADE�ա�BAO�ա�CBF
��ʱ��m��2��DE=OA=BF=m��OB=CF=AE=2��m��
��OF=BF+OB=2��
��C��������2��m��2����
��2m=2��2��m�������m=1��
�����������Ľ���ʽΪy= ![]() ��
��
��3����3,4��,y=�� ![]() x2+
x2+ ![]() ,ż��
,ż��
���������⣺��3��ʵ������������߿������ϵ���������У���һ���㶼�ڣ�3��4������࣬����������ʱ����һ�㶼�ڣ�3��4�����Ҳ࣬�������������Բ�����
�ٵ���A��x���������ϣ���B��y���������ϣ���C����Ϊ��3��4��ʱ������һ������Ϊ��4��1������Ӧ�ĺ�������ʽ��y=�� ![]() x2+
x2+ ![]() ��
��
�ڵ���A��x ���������ϣ��� B�� y���������ϣ���D ����Ϊ��3��4��ʱ�������ڣ�
�۵���A �� x ���������ϣ��� B�� y�Ḻ�����ϣ���C ����Ϊ��3��4��ʱ��������
�ܵ���A��x ���������ϣ���B��y�Ḻ�����ϣ���D����Ϊ��3��4��ʱ������һ������CΪ����1��3������Ӧ�ĺ����Ľ���ʽ��y= ![]() x2+
x2+ ![]() ��
��
�ݵ���A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���D����Ϊ��3��4��ʱ����һ������C�������ǣ�7����3��ʱ����Ӧ�ĺ�������ʽ��y=�� ![]() ��
��
����A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���C����Ϊ��3��4��ʱ����һ������D�������ǣ���4��7��ʱ����Ӧ��������Ϊy= ![]() x2+
x2+ ![]() ��
��
���������ߵİ��������εĶ���֪��һ�����������������������Σ��dzɶԳ��ֵģ�
����������κ������ߵİ��������θ���Ϊż����
�����㾫����ͨ��������������ε����ʣ������������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�ϵĵ㣬��CDB=20�㣬����C����O�����߽�AB���ӳ����ڵ�E�����E= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬ����ֱֻ�Ƿֱ���EF��DF���ۣ���Bǡ������AD���ϵĵ�B�䴦����Cǡ�����ڱ�B��F�ϣ���AE=3��BE=5����FC= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ס�����ͳʳ����Σ�ƽ��ͼ���£���λ���ף��������������������ε��棬����������������ľ�ذ壬�������������ש���������ڸ�ǽ���Ⱥ��Բ��ƣ�

��1����a��ֵ��
��2�����ú�x�Ĵ���ʽ�ֱ��ʾ���������Ҫľ�ذ�͵�ש������ƽ���ף�
��3�����г��۸�ľ�ذ嵥��Ϊ300Ԫ/ƽ���ף���ש����Ϊ100Ԫ/ƽ���ף�װ��˾��A��B���ֻ�����������
��֪����2�����Ϊ21ƽ���ף���С����Ӧѡ�����ֻ��ʹ��������ܷ��ã������ϷѼ���װ�ѣ����ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() �Ķ���
�Ķ���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() ���˶�����
���˶�����![]() ������ƽ���ڵ�����һ�㣮����
������ƽ���ڵ�����һ�㣮����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����DZ߳�Ϊ5������ʱ�����
Ϊ������ı����DZ߳�Ϊ5������ʱ�����![]() ������Ϊ__________��
������Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=BC��б��AB=4 ![]() ��O��AB���е㣬��OΪԲ�ģ��߶�OC�ij�Ϊ�뾶��Բ�Ľ�Ϊ90�������OEF��
��O��AB���е㣬��OΪԲ�ģ��߶�OC�ij�Ϊ�뾶��Բ�Ľ�Ϊ90�������OEF�� ![]() ������C����ͼ����Ӱ���ֵ����Ϊ�� ��
������C����ͼ����Ӱ���ֵ����Ϊ�� ��
A.2�Щ�4
B.4����
C.�Щ�2
D.4�Щ�8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A=84������O�ǡ�ABC����ACB��ƽ���ߵĽ��㣬��P�ǡ�BOC����OCB��ƽ���ߵĽ��㣬����P=100�������ACB�Ĵ�СΪ__________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ��������(0��1)��Ȼ����Ű�ͼ�м�ͷ��ʾ��������[��(0��0)��(0��1)��(1��1)��(1��0)����]����ÿ������һ����λ����ô�� 2020 ��ʱ��������λ�õ������ǣ� ��

A.(5��44)B.(4��44)C.(4��45)D.(5��45)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com