【题目】小明家住房户型呈长方形，平面图如下（单位：米）．现准备铺设整个长方形地面，其中三间卧室铺设木地板，其它区域铺设地砖．（房间内隔墙宽度忽略不计）

（1）求a的值；

（2）请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米；

（3）按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米．装修公司有A，B两种活动方案，如表：

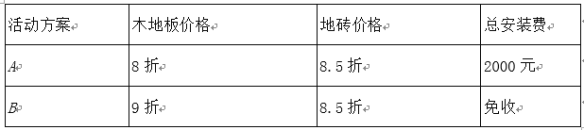
已知卧室2的面积为21平方米，则小方家应选择哪种活动，使铺设地面总费用（含材料费及安装费）更低？

参考答案：

【答案】（1）3；（2）木地板：75﹣7x，地砖：7x+53；（3）B种活动方案

【解析】

（1）根据长方形的对边相等可得a+5=4+4，即可求出a的值；
（2）根据三间卧室铺设木地板，其它区域铺设地砖，可知将三间卧室的面积的和为木地板的面积，用长方形的面积-三间卧室的面积，所得的差为地砖的面积；
（3）根据卧室2的面积为21平方米求出x，再分别求出所需的费用，然后比较即可．

解：（1）根据题意，可得a+5＝4+4，

得a＝3；

（2）铺设地面需要木地板：

4×2x+a[10+6﹣（2x﹣1）﹣x﹣2x]+6×4＝8x+3（17﹣5x）+24＝75﹣7x，

铺设地面需要地砖：

16×8﹣（75﹣7x）＝128﹣75+7x＝7x+53；

（3）∵卧室2的面积为21平方米，

∴3[10+6﹣（2x﹣1）﹣x﹣2x]＝21，

∴3（17﹣5x）＝21，

∴x＝2，

∴铺设地面需要木地板：75﹣7x＝75﹣7×2＝61，

铺设地面需要地砖：7x+53＝7×2+53＝67，

A种活动方案所需的费用：61×300×0.8+67×100×0.85+2000＝22335（元），

B种活动方案所需的费用：61×300×0.9+67×100×0.85＝22165（元），

22335＞22165，

所以小方家应选择B种活动方案，使铺设地面总费用（含材料费及安装费）更低．

关闭