
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=秒时,△PCQ的面积等于8cm2 . 
【答案】2或4或 ![]()
【解析】解:①设经过x秒,使△PCQ的面积等于8cm2,
点P在线段AC上,点Q在线段CB上(0<x≤4),
依题意有 ![]() (6﹣x)2x=8,
(6﹣x)2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
②点P在线段AC上,点Q在线段BA上(4<m<6)如图1,

设经过m秒,使△PCQ的面积等于8cm2,
则BQ=2m﹣8,AQ=18﹣2m,
过Q作QH⊥AC于H,则QH∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QH= ![]() ,
,
∴依题意有 ![]() (6﹣m)
(6﹣m) ![]() =8,
=8,
解得:m= ![]() (不合题意);
(不合题意);
③点P在线段BC上,点Q在线段AB上(6<x<9),如图2,
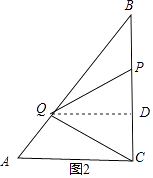
设经过n秒,使△PCQ的面积等于8cm2,
则PC=n﹣6BQ=2n﹣8,
过Q作QD⊥BC于D,则QD∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QD= ![]() ,
,
∴依题意有 ![]() (n﹣6)
(n﹣6) ![]() =8,
=8,
解得:n= ![]() ,n=
,n= ![]() (不合题意);
(不合题意);
综上所述,当t=2或4或 ![]() 秒时,△PCQ的面积等于8cm2.
秒时,△PCQ的面积等于8cm2.
所以答案是:2或4或 ![]() .
.
【考点精析】通过灵活运用平行线分线段成比例,掌握三条平行线截两条直线,所得的对应线段成比例即可以解答此题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.

(1)DE与BC是否平行,请说明理由;
(2)D、E、F分别为AB、AC、DC中点,连接BF,若![]() 四边形 ADEF=
四边形 ADEF=![]() 求
求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家住房户型呈长方形,平面图如下(单位:米).现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)

(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米.装修公司有A,B两种活动方案,如表:
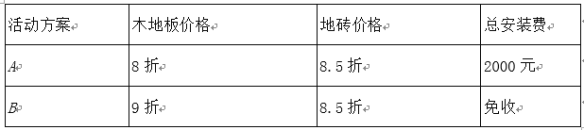
已知卧室2的面积为21平方米,则小方家应选择哪种活动,使铺设地面总费用(含材料费及安装费)更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上运动,点
上运动,点![]() 是坐标平面内的任意一点.若以
是坐标平面内的任意一点.若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是边长为5的菱形时,则点
为顶点的四边形是边长为5的菱形时,则点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4 ![]() ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF, ![]() 经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )
A.2π﹣4
B.4﹣π
C.π﹣2
D.4π﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,连结
,连结![]() 、
、![]() .点
.点![]() 是线段
是线段![]() 上的点,过点
上的点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,设AP=x.
,设AP=x.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)连结![]() ,当
,当![]() 为何值时
为何值时![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=84°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠P=100°,则∠ACB的大小为__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com