
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4 ![]() ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF, ![]() 经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )
A.2π﹣4
B.4﹣π
C.π﹣2
D.4π﹣8
【答案】A
【解析】解:连接OC,作OM⊥BC,ON⊥AC.

∵CA=CB,∠ACB=90°,点O为AB的中点,
∴OC= ![]() AB=2
AB=2 ![]() ,四边形OMCN是正方形,OM=2.
,四边形OMCN是正方形,OM=2.
则扇形FOE的面积是: ![]() =2π.
=2π.
∵OA=OB,∠AOB=90°,点D为AB的中点,
∴OC平分∠BCA,
又∵OM⊥BC,ON⊥AC,
∴OM=ON,
∵∠GOH=∠MON=90°,
∴∠GOM=∠HON,
则在△OMG和△ONH中,
 ,
,
∴△OMG≌△ONH(AAS),
∴S四边形OGCH=S四边形OMCN=22=4.
则阴影部分的面积是:2π﹣4.
所以答案是:A.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A'B'C',图中标出了点B的对应点B'.利用网格点和三角板画图:
(1)补全△A'B'C'根据下列条件;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
(4)线段A'B'与AB的关系是 .△A'B'C'的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数y= ![]() (k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 , 写出符合题意的其中一条抛物线解析式 , 并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )
A.46°
B.45°
C.44°
D.43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=秒时,△PCQ的面积等于8cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
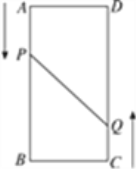
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,点
上的点,点![]() 是一动点.记
是一动点.记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() .
.
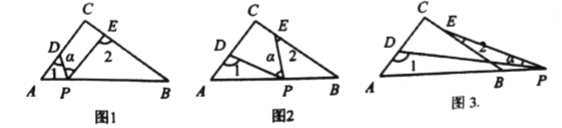
(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,如图1,则
,如图1,则![]() _____________;
_____________;
(2)若点![]() 在边
在边![]() 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想![]() ,
,![]() ,
,![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(3)若点![]() 运动到边
运动到边![]() 的延长线上,如图3所示,则
的延长线上,如图3所示,则![]() ,
,![]() ,
,![]() 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com