【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q，下列四幅图中的实线分别表示某人从A地到B地的不同行进路线（箭头表示行进的方向），则路程最长的行进路线图是（ ）

A.

B.

C.

D.

参考答案：

【答案】D

【解析】

试题分别构造出平行四边形和三角形，根据平行四边形的性质和三角形的性质进行比较，即可判断：

答如图1，A选项延长AC、BE交于S，

∵∠CAE=∠EDB=45°，∴AS∥ED. ∴SC∥DE．同理SE∥CD.

∴四边形SCDE是平行四边形. ∴SE=CD，DE=CS.

∴某人走的路线长是：AC+CD+DE+EB=AC+CS+SE+EB=AS+BS.

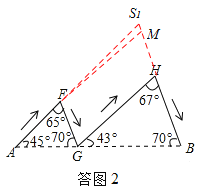
如答图2，B选项延长AF、BH交于S1，作FM∥GH，

∵∠SAB=∠S1AB=45°，∠SBA=∠S1BA=70°，AB=AB，

∴△SAB≌△S1AB. ∴AS=AS1，BS=BS1.

∵∠FGH=67°=∠GHB，∴FG∥HM.

∵FM∥GH，∴四边形FGHM是平行四边形.

∴FM=GH，FG=MH，∴AF+FG+GH+HB=AF+FM+MH+HB.

∵FS1+S1M＞FM，

∴AS1+BS1＞AF+FM+MH+MB，即AC+CD+DE+EB＞AF+FG+GH+HB.

如答图3，4，同理可证得AI+IK+KM+MB＜AS2+BS2＜AN+NQ+QP+PB.

又∵AS+BS＜AS2+BS2，故选D．

关闭