
【题目】(类比探究)如图1,线段AD,CB相交于点O,连接AB,DC,我们把形如图1的图形称之为“X型”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AE和CE相交于点E,并且与CB,AD分别相交于F,G,试解答下列问题:
(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系:____________;
(2)在图2中,共有______个“X型”;
(3)在图2中,若∠D=40°,∠B=30°,则∠AEC=_______;
(4)在图2中,若∠D=α,∠B=β,则∠AEC=__________.

【答案】(1)∠A+∠D=∠C+∠B;(2)6;(3)35°;(4)α+β.
【解析】
(1)根据三角形内角和定理即可得出∠A+∠B=∠C+∠D;
(2)根据“X型”的定义,仔细观察图形即可得出“X型”共有6个;
(3)先根据“X型”中的角的规律,可得∠BAE+∠B=∠E+∠ECB①,∠ECD+∠D=∠EAD+∠E②,再根据角平分线的定义,得出∠BAE=∠EAD,∠BCE=∠ECD,将①+②,可得2∠E=∠D+∠B,进而求出∠E的度数;
(4)同(3),根据“X型”中的角的规律及角平分线的定义,即可得出2∠AEC=α+β.
(1)∵∠A+∠B+∠AOB=∠C+∠D+∠DOC=180°,∠AOB=∠DOC,
∴∠A+∠B=∠C+∠D;
故答案为:∠A+∠D=∠C+∠B;
(2)①线段AD、CB相交于点O,形成“X型”;
②线段AG、CF相交于点O,形成“X型”;
③线段AD、CE相交于点G,形成“X型”;
④线段AD、CF相交于点O,形成“X型”;
⑤线段AE、CB相交于点F,形成“X型”;
⑥线段AG、CB相交于点O,形成“X型”;
故“X型”共有6个;
故答案为:6.
(3)∠BAE+∠B=∠E+∠ECB,①
∠ECD+∠D=∠EAD+∠E,②
∵∠DAB和∠BCD的平分线AE和CE相交于点E,
∴∠DAE=∠EAB,∠DCE=∠ECB,
①+②得:
∠BAE+∠B +∠ECD+∠D =∠E+∠ECB +∠EAD+∠E,
即2∠E=∠D+∠B,
又∵∠D=40°,∠B=30°,
∴2∠E=40°+30°=70°,
∴∠AEC=35°;
故答案为:35°;
(4)由(3)知:2∠E=∠D+∠B.
∵∠D=α,∠B=β,
∴2∠E=α+β.
故答案为:α+β.


科目:初中数学 来源: 题型:
【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )
A.46°
B.45°
C.44°
D.43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
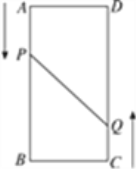
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a-2b)米的正方形,(0<b<![]() ).
).
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB= ![]() ∠C,BE⊥DE,垂足E,DE与AB相交于点F.
∠C,BE⊥DE,垂足E,DE与AB相交于点F.
(1)当AB=AC时,(如图1),
① ∠EBF=°;
②求证:BE= 1 2 FD;
(2)当AB=kAC时(如图2),求 ![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com