
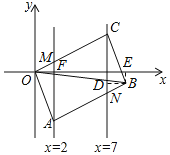
【题目】如图,已知ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为_____.

【答案】9
【解析】
过点B作BD⊥直线x=7,交直线x=7于点D,过点B作BE⊥x轴,交x轴于点E.则OB=![]() .由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,即可得出答案.
解:过点B作BD⊥直线x=7,交直线x=7于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,
直线x=7与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=7均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中, ,
,
∴△OAF≌△BCD(ASA).
∴BD=OF=2,
∴OE=7+2=9,
∴OB=![]() .
.
∵OE的长不变,
∴当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=9.
故答案为:9.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= ![]() 经过点M.
经过点M.
(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.
(2)当一次函数y=ax+2的图象与反比例函数y= ![]() 的图象有唯一公共点M,且OM=
的图象有唯一公共点M,且OM= ![]() ,求a的值.
,求a的值.
(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移 ![]() 个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A'B'C',图中标出了点B的对应点B'.利用网格点和三角板画图:
(1)补全△A'B'C'根据下列条件;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
(4)线段A'B'与AB的关系是 .△A'B'C'的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x一1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值.
(1)(x-1)(x+1) =_____________;
(2)(x—1)( x2+x+1) =_____________;
(3)(x-1)(x3+ x2+x+1) =____________;
…
由此我们可以得到:
(4)(x一1)( x99+x98+x97+…+x+1) =___________,
请你利用上面的结论,完成下列的计算:
(5)299+298+297+…+2+1;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com