【题目】如图，M是△ABC的边BC的中点，AN平分
，BN
AN于点N，延长BN交AC于点D，已知AB=10，AC=16.
（1）求证：BN=DN；
（2）求MN的长.
科目：初中数学 来源： 题型：
【题目】问题发现：数学兴趣小组在活动时，老师提出了这样一个问题：如图①，在Rt△ABC中，∠BAC＝90°，BC＝10，AD是BC边上的中线，求AD的长度．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，则AD＝
AE
在△ADC和△EDB中
∴△ADC≌△EDB
∴∠DBE＝∠DCA，BE＝AC
∴BE∥AC
∴∠EBA+∠BAC＝180°
∵∠BAC＝90°
∴∠EBA＝90°
在△EBA和△CAB中
∴△EBA≌△CAB
∴AE＝BC
∵BC＝10
∴AD＝AE＝BC＝5
（1）若将上述问题中条件“BC＝10”换成“BC＝a”，其他条件不变，则可得AD＝ ．
从上得到结论：直角三角形斜边上的中线，等于斜边的一半．
（感悟）解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形进而求解．
问题解决：（2）如图②，在四边形ABCD中，AD∥BC，∠D＝90°，M是AB的中点．若CM＝6.5，BC+CD+DA＝17，求四边形ABCD的面积．
问题拓展：（3）如图③，在平行四边形ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，∠DFE与∠AEF的度数满足数量关系：∠DFE＝k∠AEF，求k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明家住房户型呈长方形，平面图如下（单位：米）．现准备铺设整个长方形地面，其中三间卧室铺设木地板，其它区域铺设地砖．（房间内隔墙宽度忽略不计）
（1）求a的值；
（2）请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米；
（3）按市场价格，木地板单价为300元/平方米，地砖单价为100元/平方米．装修公司有A，B两种活动方案，如表：
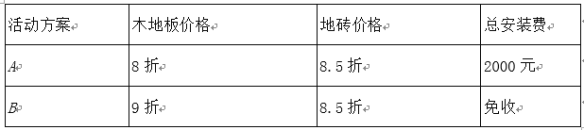
已知卧室2的面积为21平方米，则小方家应选择哪种活动，使铺设地面总费用（含材料费及安装费）更低？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某物流公司现有114吨货物，计划同时租出A，B两种型号的车，王经理发现一个运货货单上的一个信息是：
A型车（满载） | B型车（满载） | 运货总量 |
3辆 | 2辆 | 38吨 |
1辆 | 3辆 | 36吨 |
根据以上信息，解析下列问题：
（1）1辆A型车和1辆B型车都装满货物一次可分别运货多少吨？
（2）若物流公司打算一次运完，且恰好每辆车都装满货物，请你帮该物流公司设计租车方案。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，矩形
的顶点
、
的坐标分别为
，
，点
是
的中点，点
在
上运动，点
是坐标平面内的任意一点．若以
、、、为顶点的四边形是边长为5的菱形时，则点的坐标为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形
中，
，
，
、
分别是
、
上的点，且
，连结
、
．点
是线段
上的点，过点作
交
于点
，设AP=x．
（1）求证：四边形
是菱形；
（2）用含
的代数式表示
的长；
（3）连结
，当为何值时
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图是南通市1995-2001年国内生产总值增长率变化情况，下列结论不正确的是（ ）
A.1995-1998年，南通市国内生产总值的年增长率逐年减小
B.自1998年以来，南通市国内生产总值的年增长率开始回升
C.1995年-2001年，南通市每年的国内生产总值有增有减
D.1995年-2001年，南通市每年的国内生产总值不断增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
