
【题目】如图,梯形ABCD中,AB∥CD,且AB=2CD,E. F分别是AB、BC的中点,EF与BD相交于点M.

(1)求证:四边形CBED是平行四边形.
(2)若DB=9,求BM的值.
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
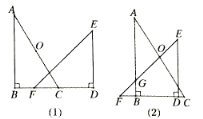
【题目】如图,为一副重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为( )
A. 3B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图是一个跳棋棋盘,其游戏规则是一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上例如:从起始位置![]() 跳到终点位置
跳到终点位置![]() 有两种不同路径,路径1:
有两种不同路径,路径1:![]() ;路径2:
;路径2:![]() .
.

试一试:(1)写出从起始位置![]() 跳到终点位置
跳到终点位置![]() 的一种路径;
的一种路径;
(2)从起始位置![]() 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置
依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为2m,宽为2n的长方形(m>n),沿图中虚线用剪刀均匀分民四块小长方形,然后按图②的形状拼成一个正方形.

(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价180元,T恤每件定价60元,厂家在开展促销活动期间,向顾客提供了两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款;现在某客户要到该厂购买夹克30件,T恤![]() 件(
件(![]() >
>![]() ).
).
(1)若该客户按方案①购买付款 元(用含![]() 的式子表示);若该客户按方案②购买付款 元(用含
的式子表示);若该客户按方案②购买付款 元(用含![]() 的式子表示).
的式子表示).
(2)当![]() 时,通过计算说明方案①、方案②哪种方案购买较为合算?
时,通过计算说明方案①、方案②哪种方案购买较为合算?
(3)当![]() 时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
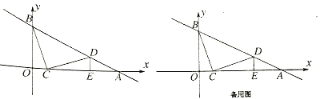
【题目】如图,在平面直角坐标系中,直线 y=kx+b与x 轴、y 轴相交干A(6,0),B(0,3)两点,动点C在线段OA上,将线段CB 绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D 作DE⊥x 轴于点E
(1)求直线y=kx+b 的表达式及点D 的坐标;
(2)若点P在y 轴上,点Q在直线AB上,是否存在以C、D、P、Q 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q 点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
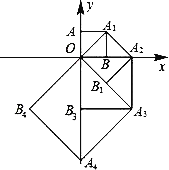
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA2A3B3,…,依此规律,则点A10的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com