
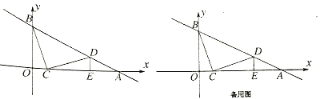
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,ֱ�� y=kx+b��x �ᡢy ���ཻ��A(6��0)��B(0��3)���㣬����C���߶�OA��,���߶�CB ���ŵ�C˳ʱ����ת90��õ�CD,��ʱ��Dǡ������ֱ��AB��,����D ��DE��x ���ڵ�E
(1)��ֱ��y=kx+b �ı���ʽ����D �����ꣻ
(2)����P��y ����,��Q��ֱ��AB��,�Ƿ������C��D��P��Q Ϊ������ı�����ƽ���ı��Σ�������,ֱ��д����������������Q �����꣬��������,��˵������.
���𰸡���1��D��4��1��;��2��Q������Ϊ![]()
![]() ��
��![]()
��������
��1���ô���ϵ���������ֱ�߽���ʽ������ת��Ϊ90������֤�á�BCO=��CDE���Ӷ��õ���BOC�ա�CED������OC=DE��BO=CE=3����OC=DE=m, ���D��m+3��m�����������ʽ���m,�����õ���D������.��2���������������ͼ�Σ����ƽ���ı��ε��������������꼴��.
�⣺
��1����A��6��0����B��0��3������ֱ��y=kx+b�ã�
![]()
��
![]() ��
��
�ߡ�BOC=��BCD=��CED=90����
���OCB+��DCE=90������DCE+��CDE=90����
���BCO=��CDE��
��BC=CD��
���BOC�ա�CED��
��OC=DE��BO=CE=3��
��OC=DE=m,
��D��m+3��m��
��D��m+3��m������![]() �ã�
�ã�
![]() ��
��
��m=1 ��
��D��4��1����
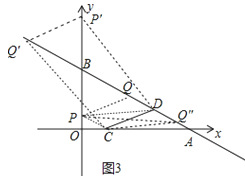
��2����ͼ������CP��AB��y����P,��PQ��CD��AB��Q,���ı���PCDQ��ƽ���ı��Σ���![]() ,��C��1��0������ã�b=
,��C��1��0������ã�b=![]() ,
,
��![]() ��
��
��P��0��![]() ����
����
�ߵ�C����ƽ��3����λ��������ƽ��1����λ�õ�D,
���P����ƽ��3����λ��������ƽ��1����λ�õ�Q,
��Q![]()
�� ��P��Q����CD��y����P��,��AB��Q��,���ı���Q��CDP����ƽ���ı��Σ�
��PQ![]() CD��P��Q��
CD��P��Q��![]() CD��
CD��
��PQ![]() P��Q����
P��Q����
��P��Q��PQ��ƽ���ı��Σ�
��Q��,Q���ڵ�B�Գƣ�
��Q��![]() ��
��
�� ��CDΪ�Խ���ʱ���ı���DPCQ���Ϊƽ���ı��Σ�
ͬ�٣���ƽ�ƿɵ�Q���![]() ��
��
��Q������Ϊ![]()
![]() ��
��![]()


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д� ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
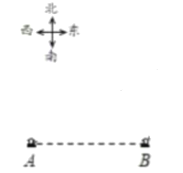
����Ŀ����ͼ��A�غ�B�ض��Ǻ��Ϲ۲�վ��B����A������������A��B�������2��� ��A�ط������ı�ƫ��60��������һ�Ҵ�C��ͬʱ����B�ط��ִ�C�����ı�ƫ��30������
��1����ͼ�л�����C���ڵ�λ�ã���Ҫ����ֱ������������ͼ��������ͼ�ۼ���
��2����֪�����ε��ڽǺ͵���180�������ACB�Ķ�����
��3����ʱ��C��B�����______�����ֻ��д�����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�A�ڲ���һ��P������BP��CP����ش��������⣺

��1����֤����P����1+��A+��2��
��2����ͼ2����������Ľ��ۣ���������У���A+��B+��C+��D+��E���� ����
��3����ͼ3������ڡ�BAC������������ͻ��Ľǣ��������ǰ��Ľ��۲����1����2����3����4����5����A֮����ʲô������ϵ��ֱ��д�����ۼ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABCD��,AB��CD����AB=2CD��E. F�ֱ���AB��BC���е㣬EF��BD�ཻ�ڵ�M.

(1)��֤���ı���CBED��ƽ���ı���.
(2)��DB=9����BM��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
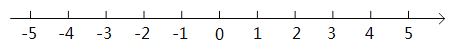
��1��̽����
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
��2�����ɣ�
һ��ģ������ϱ�ʾ��m����n������֮��ľ������ .
��3��Ӧ�ã�
�������ʾ��![]() ��3������֮��ľ�����9����ɼ�Ϊ��
��3������֮��ľ�����9����ɼ�Ϊ��![]() ����ô
����ô![]() .
.
���������ϱ�ʾ��![]() �ĵ�λ��
�ĵ�λ��![]() ��
��![]() ֮�䣬��
֮�䣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������͡����������ҡ����������������б�ʾ��������ǵ�ʽ���У���90�㩁���£��ڡ�����90����![]() ������+���£�����
������+���£�����![]() ������������������ȷ���У�������
������������������ȷ���У�������
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C�ֱ���x�ᣬy����������ϣ���OA=4��OC=3���������߾���O��A���㣬�Ҷ�����BC���ϣ��Գ��ύAC�ڵ�D������P�������߶Գ����ϣ�����Q������������
��1���������ߵĽ���ʽ��
��2����PO+PC��ֵ��Сʱ�����P�����ꣻ
��3���Ƿ������A��C��P��QΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��P��Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ��a��B��ʾ��b��C���ʾ��c��b����С������������a��b����![]() +(c��7)2=0��
+(c��7)2=0��
(1) a= ��b= ��c= ��
(2) ���������۵���ʹ��A����C���غϣ����B���� ��ʾ�ĵ��غϣ�
(3) ��A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����AB= ��AC= ��BC= ��(�ú�t�Ĵ���ʽ��ʾ)
(4) ���ʣ�3BC��2AB��ֵ�Ƿ�����ʱ��t�ı仯���ı�? ���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB���O�����ڵ�C��OA��OB�ֱ�O�ڵ�D,E����CD=��CE��
��1����֤��OA=OB
��2����֪AB=4![]() ��OA=4������Ӱ���ֵ������
��OA=4������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com